Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 73

Um vidro difuso especial, com propriedades radiantes espectrais conhecidas, é aquecido no interior de um grande forno. As paredes do forno, que são mantidas a T p = 1800   K , são revestidas com um tijolo refratário cinza e difuso que tem uma emissividade de 0,75 . Considere condições nas quais a temperatura do vidro é T v = 750   K .

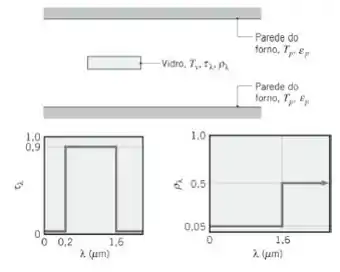
(a) Quais são a transmissividade total τ , a refletividade total ρ e a emissividade total ε do vidro?

(b) Qual é o fluxo térmico radiante líquido, q l i q , e n t ' ' ( W / m 2 ) , para o vidro?

(c) Para temperaturas da parede do forno de 1500 ,   1800 e 2000   K , represente graficamente q l i q , e n t ' '   como uma função da temperatura do vidro para 500   ≤   T v ≤   800   K .

Passo 1

Nessa questão nós temos um vidro difuso a T g =   750   K com propriedades radiativas espectrais prescritas sendo aquecidas em um forno grande com paredes com emissividade de 0,75 e 1800   K .

Com isso vamos encontrar a transmissividade total r , refletividade total ρ e emissividade total ε do vidro, o fluxo de calor radiativo líquido para o vidro e q l i q , e n t ' ' . Vamos lá!

Passo 2

Para resolver essa questão vamos assumir que:

(1) O vidro é de temperatura uniforme;

(2) O vidro é difuso;

(3) As paredes do forno são grandes em comparação com o vidro; ε w não desempenha nenhum papel;

(4) A convecção insignificante.

A partir do conhecimento da transmitância espectral, τ w e refletividade espectral, ρ λ , são avaliadas as seguintes propriedades de radiação:

Transmissividade total, τ : para a irradiação das paredes do forno, G λ =   E λ ,   b   ( λ ,   T w ) . Então,

τ = ∫ 0 ∞ τ λ E λ , b λ ,   T w σ T w 4 d λ ≈ τ λ 1 F 0 - λ   T = 0,9 × 0,25 = 0,225

Usando a tabela 12.1 para λ   T = 1,6 μ m × 18 00 K = 2 88 0 μ m . K ,   F ( 0 - λ   T ) ≈ 0,25 .

Passo 3

Já a refletividade total, ρ : Com G λ =   E λ ,   b   λ ,   T w ,   T w = 1800 K e F ( 0 - λ   T ) = 0,25

ρ ≈ ρ λ , 1 F 0 - λ   T + ρ λ , 2 1 - F 0 - λ   T = 0 , 05 × 0,25 + 0.5 1 - 0,25 = 0,388

Absortividade total, α : para executar o balanço de energia posteriormente, precisamos de α . Então, vamos usar a expressão de conservação,

α = 1 - ρ - τ = 1 - 0,388 - 0,225 = 0,387

Para concluir a letra (a), temos a emissividade, ε : Com base na temperatura da superfície T g   =   750   K , para:

λ   T = 1,6 μ m × 75 0 K = 120 0 μ m . K                                                       F ( 0 - λ   T ) ≈ 0 , 002

Então, para λ   >   1.6   μ m ,

ε ≈ ε λ ≈   0 , 5

Passo 4

Realizando um balanço de energia no vidro, o fluxo de calor radiativo líquido por radiação no vidro é,

q l i q , e n t ' ' = E e n t ' ' - E s a i ' '

q l i q , e n t ' ' = 2 α G - ε E b T g

Onde G = σ T w 4

q l i q , e n t ' ' = 2 0,387 σ 1800 K 4 - 0,5 σ 750 K 4

q l i q , e n t ' ' = 442,8   K W / m 2

Resposta

  1. τ = 0,225 ,     ρ = 0,388 e ε ≈ ε λ ≈   0,5
  2. q l i q , e n t ' ' = 442,8   K W / m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a superfície metálica do Exemplo 12.7. Medições adicionais da emissividade hemisférica espectral fornecem uma distribuição espectral que pode ser aproximada como a seguir:(a) Determine os va
Uma superfície opaca e difusa, a 680K , tem emissividades espectrais ε λ = 0 para 0 ≤ λ ≤ 3μ m ; ε λ = 0 , 4 para 3λ ≤ 10μ m ; e ε λ = 0 , 7 para 10λ∞ . Um fluxo radiante de 1000W / m 2 , uniformement
Um pequeno objeto opaco e difuso, a T s = 5 00K , está suspenso em um grande forno cujas paredes internas estão a T f = 2 5 00K . As paredes são difusas e cinzas, e têm uma emissividade de 0 , 37 . A
Dois revestimentos especiais estão disponíveis para aplicação em uma placa de absorção instalada abaixo da cobertura de vidro descrita no Exemplo 12.9. Cada um dos revestimentos é difuso e caracteriza
Uma amostra muito pequena de uma superfície opaca encontra-se inicialmente a 1200K e tem a absortividade hemisférica espectral mostrada na figura.A amostra é colocada no interior de um grande comparti