Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 71
Uma superfície difusa, que apresenta as características espectrais a seguir, é mantida a quando localizada no interior de um grande forno cujas paredes são mantidas a :
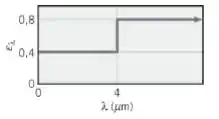
(a) Esboce a distribuição espectral do poder emissivo da superfície e do poder emissivo que a superfície teria caso ela fosse um corpo negro.
(b) Desprezando efeitos convectivos, qual é o fluxo térmico líquido para a superfície nas condições especificadas?
(c) Represente graficamente o fluxo térmico líquido como uma função da temperatura superficial para . No mesmo sistema de coordenadas, represente os fluxos térmicos para uma superfície difusa e cinza com emissividades totais de e .
(d) Para a distribuição espectral de fornecida, como a emissividade e a absortividade totais da superfície variam com a temperatura no intervalo ?
Passo 1
Oi oi OII, turubom? Nessa questão nós temos a temperatura e características espectrais de uma superfície difusa a situada em um recinto grande com temperatura uniforme, .
E com isso vamos encontrar o fluxo de calor líquido para a superfície, .
Passo 2
Para resolver essa questão vamos assumir que:
(1) A superfície é difusa;
(2) Os efeitos convectivos são desprezíveis;
(3) A irradiação da superfície corresponde à emissão do corpo negro a .
De um balanço energético na superfície, o fluxo líquido de calor para a superfície é,
Da equação 12.52,
Usando a tabela 12.1 para Então,
Passo 3
Da Eq. 12.43,
Usando a tabela 12.1 para Então,
Portanto, o fluxo líquido de calor para a superfície é,
Resposta
(b)