Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 69
Uma placa horizontal opaca tem uma espessura de e condutividade térmica de Água escoa em contato com a superfície inferior da placa e está a uma temperatura de . Ar escoa acima da placa a , com A parte superior da placa é difusa e é irradiada com , dos quais são refletidos. As temperaturas em regime estacionário das superfícies superior e inferior da placa são e , respectivamente. Determine a transmissividade, a refletividade, a absortividade e a emissividade da placa. A placa é cinza? Qual é a radiosidade associada à superfície superior da placa? Qual é o coeficiente convectivo de transferência de calor associado ao escoamento da água?
Passo 1
Nessa questão nós temos a espessura, condutividade térmica e temperaturas da superfície de uma placa plana. Assim como, sua irradiação na superfície superior, irradiação refletida, temperatura do ar e da água e coeficiente de convecção do ar.
A partir disso queremos encontrar a transmissividade, refletividade, absortividade e emissividade da placa, a radiosidade da superfície e o coeficiente de convecção associado ao fluxo de água, beleza? Então vamos lá!
Passo 2
Para resolver essa questão vamos assumir que a superfície é opaca e difusa e a água é opaca à radiação térmica. O prato é opaco então,
Já a refletividade é,
E a absorção é,
Passo 3
Considerando um balanço de energia na superfície superior,
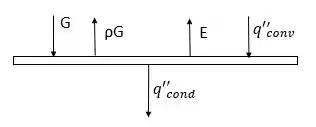
Onde,
Reorganizando, vemos que,
Substituindo os valores encontramos,
Como , a placa não é cinza
Passo 4
A radiosidade associada à superfície superior é,
Substituindo os valores,
Considerando um balanço de energia na superfície inferior com,
Temos,
Substituindo os valores,
Resposta
Como , a placa não é cinza.