Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 47

Considere um tubo circular horizontal com parede delgada e diâmetro D = 0,025   m , submerso em um recipiente que contém n-octadecano (parafina), que é usada para armazenar energia térmica. À medida que água quente escoa através do tubo, calor é transferido para a parafina, convertendo-a do estado sólido para o estado líquido na temperatura de mudança de fase T ∞ = 27,4 ° C . 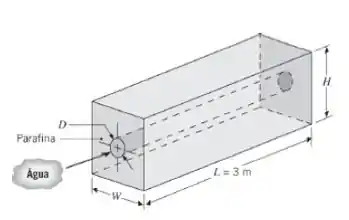O calor latente de fusão e a massa específica da parafina são h s f = 244   k J / k g e ρ = 770   k g / m 3 , respectivamente, e as propriedades termofísicas da água são: c p = 4,185   k J /   ( k g · K ) , k = 0,653   W /   ( m · K ) , μ = 467 × 10 – 6   k g /   ( s · m ) e P r = 2,99 .

a) Supondo que a superfície do tubo tenha uma temperatura uniforme que corresponde àquela da mudança de fase, determine a temperatura de saída da água e a taxa de transferência de calor total para uma vazão de água de 0,1   k g / s e uma temperatura de entrada de 60 ° C . Se H = W = 0,25   m , quanto tempo irá levar para a liquefação completa da parafina, partindo de um estado inicial no qual toda a parafina encontra-se no estado sólido a uma temperatura de 27,4 ° C ?

Passo 1

Letra a)

Começamos o problema calculando o número de Reynolds:

R e D = 4 m ˙ μ π D

Sendo:

m ˙ = 0,1   k g / s ;

μ = 467 × 10 – 6   k g / ( s · m ) ;

D = 0,025   m .

Temos:

R e D = 4 ⋅ 0,1 467 × 10 – 6 ⋅ π   ⋅ 0,025

R e D = 10906

Calculando o número de Nusselt:

N u D = 0,023 R e D 0,8 P r f 0,3

Sendo:

P r = 2,99 .

Temos:

N u D = 0,023 ⋅ 10906 0,8 ⋅ 2,99 0,3

N u D = 54,3

Calculando o coeficiente de transferência de calor por convecção:

N u D = h D k = 54,3

Com:

k = 0,653   W / ( m · K ) .

Temos que h é:

h ⋅ 0,025 0,653 = 54,3

h = 1418   W / m 2 ⋅ K

Passo 2

Calculando a temperatura média de saída:

T ∞ - T m , s a i T ∞ - T m , e n t = exp ⁡ - π D L m ˙ c p h

Isolando T m ,   s a i :

T m , s a i = T ∞ - ( T ∞ - T m , e n t ) exp ⁡ - π D L m ˙ c p h

Dados:

T ∞ = 27,4 ° C ;

T m , e n t = 60 ° C ;

L = 3   m ;

c p = 4,185   k J / ( k g · K ) .

Temos:

T m , s a i = 27,4 - ( 27,4 - 60 ) exp ⁡ - π ⋅ 0,025 ⋅ 3 0,1 ⋅ 4185 ⋅ 1418

T m , s a i = 42,1 ° C

Passo 3

Calculando a taxa de transferência de calor:

q = m ˙ c p ( T m , e n t - T m , s a i )

Substituindo os dados:

q = 0,1 ⋅ 4185 ⋅ ( 60 - 42,1 )

q = 7491   W

Passo 4

Calculando o volume da parafina:

V = L W H - π D 2 4

Sendo:

H = W = 0,25   m .

Temos:

V = 3 ⋅ 0,25 ⋅ 0,25 - π ⋅ 0,025 2 4

V = 0,186   m 3

Calcule o tempo que irá levar para a liquefação completa da parafina:

q = ρ V h s f t

t = ρ V h s f q

Dados:

ρ = 770   k g / m 3 ;

h s f = 244   k J / k g .

Temos:

t = 770 ⋅ 0,186 ⋅ ( 244 × 10 3 ) 7491

t = 4665   s

Resposta

T m , s a i = 42,1 ° C

q = 7491   W

t = 4665   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar (1 atm) entrou em um tubo circular de 5 mm de diâmetro a uma velocidade média de 5 m/s. A parede do tubo é mantida a uma temperatura de superfície constante. Determine o coeficiente de transferênci
Ar c p = 1007 J k g K entra em um tubo de 17 cm de diâmetro e 4 m de comprimento a 65°C de temperatura e taxa de 0,08 k g s e sai a 15°C. O tubo é quase isotérmico a 5°C. O coeficiente médio de transf
Água c p = 4180 J k g K entra em um tubo de 12 cm de diâmetro e 8,5 m de comprimento, a uma temperatura de 75°C e uma taxa de 0,35 k g s , sendo resfriada por um refrigerante evaporando a -10°C. Se o
A água entra em um tubo de 5 mm de diâmetro e 13 m de comprimento a 45°C com velocidade de 0,3 m/s. O tubo é mantido a uma temperatura constante de 5°C. O comprimento necessário do tubo para que a águ
Ar a 110°C entra em um duto de 18 cm de diâmetro e 9 m de comprimento com velocidade de 4,5m/s. O duto é quase isotérmico a 85°C. A taxa de perda de calor do ar no duto é: 760W ; 890W ; 1210W ; 1370W