Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 35
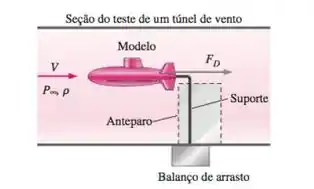
Uma equipe de alunos deve criar um submarino com energia humana para um concurso de projetos. O comprimento total do protótipo do submarino é de 2,24 m, e seus alunos projetistas esperam que ele possa viajar totalmente submerso através da água a 0,560 m/s. A água é doce (um lago) a T = 15°C. A equipe de projeto constrói um modelo em escala 1 para 8 para ser testado no túnel de vento de sua universidade. Um anterparo cerca o suporte do balanço de arrasto para que o arrasto aerodinâmico do próprio suporte não influencie o arrasto medido. O ar no túnel de vento está a 25°C e a uma pressão atmosférica padrão. Com que velocidade do ar eles precisam fazer o túnel de vento funcionar para atingir a semelhança?
Passo 1
Uma maravilha que acontece entre os números adimensionais é que eles devem ser iguais quando se fala de protótipo e modelo.
O enunciado tá pedindo pra gente pra calcular a velocidade!! E adivinha qual será o carinha adimensional que vai nos ajudar?? TCHARAMMMMM!!! TITIO REYNOLDS
Agora, vamos usar as propriedades da água a 15°C e Patm que podem ser obtidas em qualquer tabela de propriedades. (protótipo).
Também precisaremos das propriedades a 25°C (modelo).
Passo 2
Vamos então isolar a velocidade do modelo, beleza?
Agora é ser feliz, mas antes lembrar que a razão Lp/Lm = 8 !!!!