Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 46
Considere um ventilador centrífugo que tem raio de 20 cm e lâmina com largura de 8,2 cm na entrada do impulsor, e um raio de 45 cm e uma pá com largura de 5,6 cm na saída. O ventilador fornece ar a uma taxa de 0,70 m³/s a velocidade rotacional de 700 rpm. Considerando que o ar entra no impulsor na direção radial e sai com um ângulo de 50° na direção radial, determine o consumo mínimo de potência do ventilador. Tome a densidade do
ar como 1,25 kg/m³
Passo 1
Bora começar, galerinha!
A questão ta pedindo o consumo mínimo, então o que a gente tem que calucular é esse carinha aqui ó:
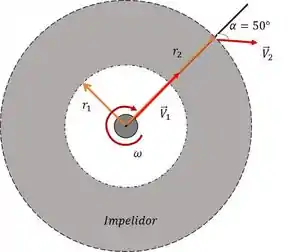
Vamos dar uma olhadinha no esquema, porque sempre ajuda:
Mas como a gente chega lá!? Bora lá!
Primeiro de tudo, a região do impelidor vai ser nosso volume de controle, ok?! Então podemos calcular as velocidades normais de entrada, , e de saída :
Sabendo essas velocidades a gente vai ser capaz de calcular as velocidades tangenciais de acordo com essa relação aqui:
Para isso precisamos só conhecer esse e !! Tão vendo essa linha verde na imagem? Essa vai ser a nossa normal, vai ser o ângulo entre a velocidade e a normal, logo é só olhar a imagem e ver que a velocidade ta juntinho com a normal, então:
Já para :
Sabendo as velocidades tangenciais, a gente pode ir pro próximo passo!
Agora a gente vai atrás da velocidade angular :
Agora a vazão mássica:
Com isso podemos achar pra finalmente substituir na fórmula de potência!!
Então vamos colocar a mão na massa pra calcular essa galera ai!
Passo 2
Primeiro as velocidades normais e :
Agora vamos achar as velocidades tangenciais :
A velocidade angular:
Repaparam na troca de rpm para rotações por segundo?Bastante atenção nas unidades!!
Precisamos da vazão mássica para....
Agora podemos calcular o torque do eixo:
E por fim, tcharaaam, o !
Resposta
O consumo mínimo de potência do ventilador será igual a