Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 185

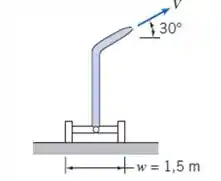
Um grande dispositivo de irrigação montado sobre um carrinho descarrega um jato de água com velocidade de 40   m / s a um ângulo de 30 ° com a horizontal. O bocal de 50   m m de diâmetro está 3   m acima do solo. A massa do dispositivo mais o carrinho é m = 350   k g . Calcule o módulo do momento que tende a tombar o carrinho. Que valor de V levará à condição de movimento iminente do carrinho? Qual será a natureza desse movimento? Qual é o efeito do ângulo de inclinação do jato sobre os resultados? Para o caso de movimento iminente do carrinho, trace um gráfico da velocidade do jato como função do seu ângulo de inclinação, para uma faixa apropriada de ângulos do jato.

Passo 1

A equação do momento angular se dá:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. T e i x o = 0 ;
  2. Fluxo Constante ∂ ∂ t = 0 ;
  3. Escoamento Uniforme.

Passo 2

Pelas considerações feitas no passo 1, temos:

r × F s + ∫ V C r × g ρ d ∀   = ∫ S C r × V   ρ V d A

Integrando:

r × F s + r × m g   = r 1 × V 1   - ρ V 1 A 1 + r 2 × V 2   ( ρ V 2 A 2 )

Pela ilustração dada, temos que r 1 × V 1 = 0 , r 2 = w 2 î + h j ^ , V 2 = V 2 ( cos ⁡ θ î + s e n   θ j ^ ) e que ρ V 2 A 2 = m 2 ˙ .

r × F s + r × m g   = w 2 î + h j ^ ⋅ V 2 cos ⁡ θ î + s e n   θ j ^ ⋅   m 2 ˙

Substituindo r × F s = w N 4 k ^ e r × m g = - w 2 m g k ^ , obtemos a equação:

( w N 4 - w 2 m g ) k ^   = m 2 ˙ V 2 w 2 s e n   θ - h   c o s   θ k ^

Passo 3

Precisamos calcular m 2 ˙ .

m 2 ˙ = ρ A 2 V 2 = ρ π D 2 V 2 4

Sendo:

ρ = 1000   k g / m 3 ;

D = 0,05   m ;

V 2 = 40   m / s .

Temos:

m 2 ˙ = 1000 ⋅ π ⋅ 0,05 2 ⋅ 40 4 = 78,5   k g / s

Passo 4

Calculando o módulo do momento que tende a tombar o carrinho.

m o m e n t o = - m 2 ˙ V 2 w 2 cos ⁡ θ - h s e n   θ

Sendo:

m 2 ˙ = 78,5   k g / s ;

V 2 = 40   m / s ;

w = 1,5   m ;

h = 3   m ;

θ = 30 ° .

Temos:

m o m e n t o = - 78,5 ⋅ 40 1,5 2 s e n   30 ° - 3   c o s   30 ° = - 6,98   k N ⋅ m

Passo 5

Calculando o valor de v que levará à condição de movimento iminente do carrinho.

Para iminência N 4 → 0 , então:

- w 2 m g   = m 2 ˙ V 2 w 2 s e n   θ - h   c o s   θ

Rearranjando:

V 2 = - w 2 m g ρ π D 2 4 w 2 s e n   θ - h cos ⁡ θ

Com dos dados apresentados anteriormente e com g = 9,8   m / s 2 e m = 350   k g , temos:

V 2 = - 1,5 2 ⋅ 350 ⋅ 9,8 1000 ⋅ π ⋅ 0,05 2 4 1,5 2 s e n   30 ° - 3 cos ⁡ 30 ° = 24,3   m / s

A natureza do movimento será angular.

A ângulo de inclinação tem o efeito de ditar a velocidade do jato.

Passo 6

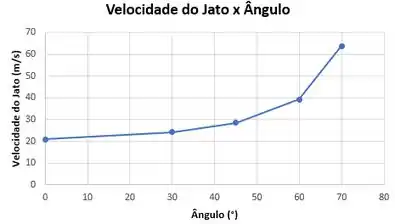
Traçando um gráfico da velocidade do jato como função do seu ângulo de inclinação, para uma faixa apropriada de ângulos do jato

Resposta

m o m e n t o = - 6,98   k N ⋅ m

V 2 = 24,3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jato d’água horizontal de um bocal com seção transversal de saída constante atinge normalmente uma placa plana vertical e fixa. Determinada força F é necessária para manter a placa contra a corrent
Descreva por que um helicóptero flutua no ar em termos do momento e do escoamento de ar.
Um jato d’água horizontal com 5c m de diâmetro e velocidade de 30m / s atinge uma placa plana fixa vertical. A água se espalha em todas as direções no plano da placa. Qual a força necessária para mant
A água entra em uma bomba de escoamento mista axialmente a uma taxa de 0,2m 3 / s e a uma velocidade de 5 m s , e é descarregada para a atmosfera a um ângulo de 60 ° da horizontal, como mostra a figur
Um jato d’água horizontal, com taxa de escoamento V ˙ e área de seção transversal A , movimenta um carrinho coberto de massa m c ao longo de uma trajetória nivelada e quase sem atrito. O jato entra em