Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 55

Uma corrente elétrica escoa por uma barra longa, gerando energia térmica a uma taxa volumétrica uniforme de q ˙ = 2 x 10 6   W / m 3 . A barra é concêntrica com um cilindro de cerâmica oco, criando um espaço cheio de ar entre os dois.

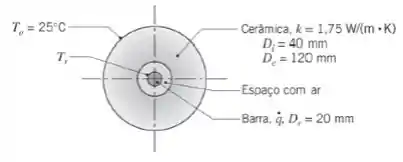
A resistência térmica por unidade de comprimento devido à radiação entre as superfícies do espaço barra/cerâmica é igual a R r a d ' = 0,30   m · K / W e o coeficiente associado à convecção natural neste mesmo espaço é de h = 20   W / ( m 2 · K ) .

a) Construa um circuito térmico que possa ser utilizado para calcular a temperatura superficial da barra, T b . Identifique todas as temperaturas, as taxas de transferência de calor e as resistências térmicas, e calcule cada resistência térmica.

b) Calcule a temperatura superficial da barra para as condições especificadas.

Passo 1

Letra a)

O circuito térmico se dá da seguinte maneira:

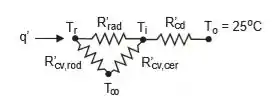
Passo 2

Calculando as resistências térmicas por radiação e convecção livre que formam a resistência equivalente:

  • R r a d ' é apresentada no enunciado com 0,30   m · K / W ;
  • R c v , r o d ' é dada por:

R c v , r o d ' = 1 π D r h

Dados:

D r = 20   m m = 0,02   m ;

h = 20   W / ( m 2 · K ) .

Temos:

R c v , r o d ' = 1 π ⋅ 0,02 ⋅ 20 = 0,8   m ⋅ K / W

  • R c v , c e r ' é dada por:

    • R c v , c e r ' = 1 π D i h

    Com:

    D i = 40   m m = 0,04   m .

    Temos:

    R c v , c e r ' = 1 π ⋅ 0,0 4 ⋅ 20 = 0 , 4   m ⋅ K / W

    A resistência equivalente a essas três apresentadas anteriormente se dá por:

    1 R e q ' = 1 R r a d ' + 1 R c v , r o d ' + R c v , c e r '

    Substituindo os dados:

    1 R e q ' = 1 0,3 + 1 0,8 + 0,4

    R e q ' = 0,24   m ⋅ K / W

    Passo 3

    Calculando a resistência por condução e a total:

  • R c d ' é dada por:

    • R c d ' = ln ⁡ D e D i 2 π k

    Dados:

    D e = 120   m m = 0,12   m ;

    k = 1,75   W / m ⋅ K .

    Temos:

    R c d ' = ln ⁡ 0,12 0,04 2 π ⋅ 1,75 = 0,10   m ⋅ K / W

  • A R t o t a l ' é a soma da resistência equivalente com a pôr condução:

R t o t a l ' = R e q ' + R c d '

R t o t a l ' = 0,24 + 0,10

R t o t a l ' = 0,34   m ⋅ K / W

Passo 3

Letra b)

Para calcularmos a temperatura superficial da barra, temos que aplicar um balanço de energia primeiramente:

E ˙ e n t ' - E ˙ s a i ' + E ˙ g e r ' = 0

Com não há entrada de energia, há apenas a energia gerada e a que saí, obtemos:

- q + q ˙ ∀ = 0

Estendendo:

- T s - T o R t o t a l ' + q ˙ ⋅ π D r 2 4 = 0

T s - T o R t o t a l ' = q ˙ ⋅ π D r 2 4

Isolando T s :

T s = R t o t a l ' ⋅ q ˙ ⋅ π D r 2 4 + T o

Dados:

R t o t a l ' = 0,34   m ⋅ K / W ;

  q ˙ = 2 x 10 6   W / m 3 ;

D r = 20   m m = 0,02   m ;

T o = 25 ° C = 298   K .

Temos:

T s = 0,34 ⋅ ( 2 x 10 6 ) ⋅ π ⋅ 0,02 2 4 + 298

T s = 511,6   K = 238,6 ° C

Resposta

R t o t a l ' = 0,34   m ⋅ K / W

T s = 511,6   K = 238,6 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um tubo isolado exposto à atmosfera. O raio crítico do isolamento será maior em dias calmos ou em dias ventosos? Por quê?
Repita o Problema 3–84 para oxigênio líquido, que tem uma temperatura de ebulição de -183°C, calor de vaporização de 213 k J k g e densidade de 1140 k g m 3 a 1 atm de pressão.
Repita o Problema 3-80, considerando que a camada de 0,25 cm de espessura de depósito mineral k = 0,87Wm· K se formou sobre a superfície interna do tubo.
A temperatura de ebulição à pressão atmosférica do nitrogênio ao nível do mar (pressão de 1 atm) é -196°C. Portanto, o nitrogênio é comumente usado em estudos científicos de baixa temperatura. A tempe
Um fio elétrico de 2,2 mm de diâmetro e 14 m de comprimento é enrolado firmemente com uma cobertura plástica de 1 mm de espessura cuja condutividade térmica ék =0,15Wm·K . As medições elétricas indica