Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 83

A temperatura de ebulição à pressão atmosférica do nitrogênio ao nível do mar (pressão de 1 atm) é -196°C. Portanto, o nitrogênio é comumente usado em estudos científicos de baixa temperatura. A temperatura do nitrogênio líquido em um tanque aberto para a atmosfera permanecerá constante a -196°C até que seja consumido. Qualquer transferência de calor para o tanque resultará na evaporação de algum nitrogênio líquido, que possui um calor de vaporização de 198 k J k g e densidade de 810 k g m 3 a 1 atm.

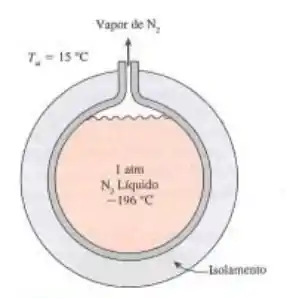
Considere um tanque esférico de 3 m de diâmetro que é inicialmente preenchido com nitrogênio líquido a 1 atm e -196°C. O tanque é exposto ao ar ambiente a 15°C, com um coeficiente combinado de transferência de calor por convecção e radiação de 35 W m 2   ·   K . A temperatura da fina casca do tanque esférico deve ser quase a mesma que a temperatura do nitrogênio no interior. Determine a taxa de evaporação do nitrogênio líquido no tanque como resultado da transferência de calor do ar ambiente se o tanque for:

  1. Não isolado;
  2. Isolado com isolamento de fibra de vidro de 5 cm de espessura k = 0,035 W m   ·   K ;
  3. Isolados com superisolante de 2 cm de espessura que possui uma condutividade térmica efetiva de 0,00005   W m   ·   K .

Passo 1

Bora começar !! Apesar de grande, esta aqui não é nada complicada.

Na letra a nós temos apenas uma fina camada do tanque, sem nenhum isolamento.

Como a temperatura do tanque esférico de casca fina é quase igual à temperatura do nitrogênio no interior nós podemos concluir que a resistência térmica do tanque e a resistência de convecção interna são desprezíveis.

Então o que nós teremos aqui?

Então basta calcularmos a resistência externa:

R e x t = 1 h e x t × A e x t

No caso de sólidos esféricos a área é calculada como:

A e x t = π d 1 2

Na fórmula:

R e x t = 1 h e x t × π d 1 2

Substituindo os valores:

R e x t = 1 35 W m 2   ·   K × π 3   m 2 = 0,00101 K W

Lembrando que o calor é dado por:

Q ˙ = T e x t - T s u p ,   e x t R e x t

Substituindo:

Q ˙ = 15 ° C - ( - 196 ° C ) 0,00101 K W

Como a variação em graus Celsius e kelvin é a mesma:

Q ˙ = 208910,9   W

Ou melhor:

Q ˙ = 208,910   k W = 208,910 k J s

Achamos o que precisávamos?

Claro que não né? É preciso saber da taxa de nitrogênio que evapora.

Então basta usarmos a fórmula do calor de vaporização:

Q ˙ = m ˙ h v a p

Lembrando que:

h v a p = 198 k J k g

Substituindo os dados:

m ˙ = 208,910   k J s 198 k J k g = 1,055 k g s

Agora sim !! Achamos a letra (a) !!

Passo 2

Na letra b nós temos um isolamento, ou seja, duas resistências.

Também aumentamos o diâmetro para d 2 , certo?

d 2 = 3   m + 2 × 0,05   m = 3,1   m

A resistência externa passa a ser:

R e x t ,   2 = 1 h e x t × π d 2 2

Substituindo os valores:

R e x t ,   2 = 1 35 W m 2   ·   K × π 3,1   m 2 = 0,000946   K W

Ainda precisamos achar a resistência do isolamento, certo?

Como o tanque é esférico:

R i s o l a m e n t o = r 2 - r 1 4 π k r 2 r 1

Lembrando que r = d 2 e substituindo nossos dados:

R i s o l a m e n t o = 3,1   m 2 - 3,0   m 2 4 π 0,035 W m   ·   K 3,1   m 2 3,0   m 2 = 0,04 8 9 2 K W

A resistência total será:

R t o t a l = R e x t ,   2 + R i s o l a m e n t o

R t o t a l = 0,000946   K W + 0,04 8 9 2 K W = 0,0498   K W

Na fórmula do calor:

Q ˙ = 15 ° C - ( - 196 ° C ) 0,0498   K W = 4236,95   W

Ou melhor:

Q ˙ = 4,237   k W = 4,237 k J s

Usando a fórmula de vaporização:

m ˙ = 4,237 k J s 198 k J k g = 0,0214   k g s

Achamos mais umaaa !!

Passo 3

Na letra c nós temos um superisolamento, ou seja, mesmo caso que a anterior mas valores diferentes!

Animados para repetir??

Agora o diâmetro é d 3 :

d 3 = 3   m + 2 × 0,02   m = 3,04   m

A resistência externa passa a ser:

R e x t ,   3 = 1 h e x t × π d 3 2

Substituindo os valores:

R e x t ,   3 = 1 35 W m 2   ·   K × π 3,04   m 2 = 0,000984   K W

Ainda precisamos achar a resistência do isolamento, certo?

Como o tanque é esférico:

R s u p e r   i s o l a m e n t o = r 3 - r 1 4 π k r 3 r 1

Lembrando que r = d 2 e substituindo nossos dados:

R s u p e r   i s o l a m e n t o = 3,04   m 2 - 3,0   m 2 4 π 0,00005   W m   ·   K 3,04   m 2 3,0   m 2 = 13,96 K W

A resistência total será:

R t o t a l = R e x t , 3 + R s u p e r   i s o l a m e n t o

R t o t a l = 0,000984   K W + 13,96 K W = 13,96   K W

Na fórmula do calor:

Q ˙ = 15 ° C - ( - 196 ° C ) 13,96   K W = 15,11   W

Ou melhor:

Q ˙ = 0,01511   k W = 0,01511 k J s

Usando a fórmula de vaporização:

m ˙ = 0,01511 k J s 198 k J k g = 0,000076   k g s

E é isso aí, galera !!

Agora finalizamos !!

Resposta

  1. 1,055 k g s ;
  2. 0,0214   k g s ;
  3. 0,000076   k g s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Feixes de laser são usados para processar termicamente materiais em uma ampla gama de aplicações. Frequentemente, o feixe é deslocado ao longo da superfície do material segundo um padrão desejado. Sej
Condução bidimensional, em regime estacionário, ocorre em um sólido cilíndrico oco de condutividade térmica k = 22W / ( m · K ) , raio externo r e = 1 , 5m e comprimento total 2 z e = 8m , onde a orig
Um fino aquecedor elétrico é envolvido em torno da superfície externa de um longo tubo cilíndrico cuja superfície interna é mantida a uma temperatura de 6 ℃ ℃. A parede do tubo tem raios internos e ex
Use a análise de condução alternativa da Seção 3.2 para derivar uma expressão relacionando a taxa de calor radial, q r , às temperaturas da parede T s , 1 e T s , 2 , para o cilindro oco da Figura 3.7
Uma esfera oca de alumínio, com um aquecedor elétrico no centro, é usada em testes para determinar a condutividade térmica de materiais isolantes. Os raios interno e externo da esfera são 0,18 e 0,21m