Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 61

Vapor d’água escoando em um longo tubo, com parede delgada, mantém a sua parede a uma temperatura uniforme de 500   K . O tubo é coberto por uma manta de isolamento composta por dois materiais diferentes, A e B.

Pode-se supor que há, na interface entre os dois materiais, uma resistência de contato infinita. Toda a superfície externa está exposta ao ar, para o qual T ∞ = 300   K e h = 25   W / ( m 2 · K ) .

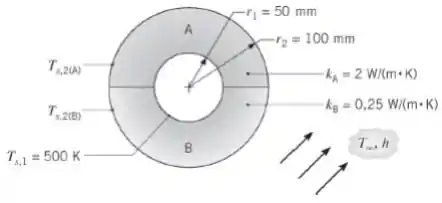
a) Esboce o circuito térmico do sistema. Identifique (usando os símbolos propostos) todos os nós e resistências pertinentes.

b) Para as condições especificadas, qual é a perda de calor total para o ambiente? Quais são as temperaturas na superfície externa, T s , 2 A e T s , 2 B ?

Passo 1

Letra a)

Esboçando o circuito térmico do sistema:

R c o n v ' A = R c o n v ' B = 1 π r 2 h

R c o n d ' A = ln ⁡ r 2 r 1 π k A

R c o n d ' B = ln ⁡ r 2 r 1 π k B

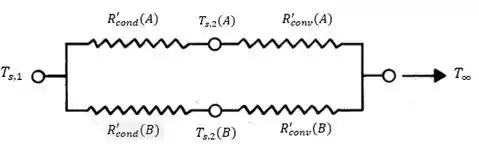
Passo 2

Letra b)

Calculando a perda de calor total para o ambiente.

Primeiramente calcularemos as resistências apresentadas no Passo 1:

Dados:

r 1 = 50   m m = 0,05   m ;

r 2 = 100   m m = 0,1   m ;

h = 25   W / ( m 2 · K ) ;

k A = 2   W / m ⋅ K ;

k B = 0,25   W / m ⋅ K .

Temos:

R c o n v ' A = R c o n v ' B = 1 π ⋅ 0,1 ⋅ 25 = 0,1273   m ⋅ K / W

R c o n d ' A = ln ⁡ 0,1 0,05 π ⋅ 2 = 0,1103   m ⋅ K / W

R c o n d ' B = ln ⁡ 0,1 0,05 π ⋅ 0,25 = 0,8825   m ⋅ K / W

Assim, a perda de calor total se dá:

q ' = q ' A + q ' ( B )

q ' = T s , 1 - T ∞ R c o n d ' A + R c o n v ' A + T s , 1 - T ∞ R c o n d ' B + R c o n v ' B

Dados:

T s , 1   = 500   K ;

T ∞ = 300   K .

Temos:

q ' = 500 - 300 0,1103 + 0,1273 + 500 - 300 0,8825 + 0,1273

q ' = 1040   W / m

Passo 3

As temperaturas na superfície externa, T s , 2 ( A ) e T s , 2 ( B ) são:

q ' = T s , 1 - T s , 2 R c o n d '

Isolando T s , 2 :

T s , 2 = T s , 1 - q ' R c o n d '

Substituindo os dados para ( A ) e ( B ) :

T s , 2 ( A ) = T s , 1 - q ' ( A ) R c o n d ' ( A )

T s , 2 A = 500 - 842 ⋅ 0,1103

T s , 2 A = 407   K = 134 ° C

T s , 2 ( B ) = T s , 1 - q ' ( B ) R c o n d ' ( B )

T s , 2 B = 500 - 198 ⋅ 0,8825

T s , 2 B = 325   K = 52 ° C

Resposta

a )   E s b o ç o   e   E q u a ç õ e s

b )   q ' = 1040   W / m

T s , 2 A = 407   K = 134 ° C

T s , 2 B = 325   K = 52 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Problema 3-76. Usando o software EES (ou outro programa), investigue o efeito da espessura do isolamento sobre a taxa de perda de calor do vapor e a queda de temperatura na camada de iso
Reconsidere o Problema 3-78 considerando um tubo feito de cobre k =386Wm· K em vez de ferro fundido.
A água refrigerada entra em um tubo de parede fina de 4 cm de diâmetro e 200 ml de comprimento a 7°C a uma taxa de 0,98 k g s e sai a 8°C. O tubo é exposto ao ar ambiente a 30°C com um coeficiente de
Vapor sai a 40°C da turbina de uma central elétrica a vapor para ser condensado em um grande condensador por água de resfriamento fluindo através dos tubos de cobre k =386Wm· K de diâmetro interno de
O vapor superaquecido a uma temperatura de 200°C é transportado através de um tubo de aço k =50Wm·K ,D e = 8,0c m ,D i = 6,0c meL = 20m . O tubo é isolado é isolado com uma camada de 4 cm de espessura