Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 8.Exercício - Ex. 8
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Dados: ; ; ; .
Desprezar as perdas e supor o diagrama de velocidades uniforme na seção.
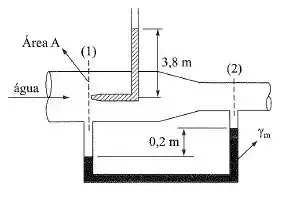
Passo 1
Vamos começar o exercício aplicando a equação manométrica entre os pontos 1 e 2:
Substituindo os valores dados no enunciado, temos:
Passo 2
Agora podemos aplicar o equilíbrio de energia entre os pontos 0 (pouco antes da entrada do tubo) e 1:
Substituindo os valores conhecidos, temos:
Passo 3
Agora, já que o enunciado disse que o diagrama de velocidades na seção é uniforme, basta aplicar a equação da vazão direto para obter o valor da vazão volumétrica, então, temos:
Resposta
Exercícios de Livros Relacionados
Querosene a 20°C escoa a 20 m³/h em um tubo de 8 cm de diâmetro. O escoamento deve ser medido por meio de um bocal ISA 1932 de modo que a queda de pressão seja 7kPa. Qual é o diâmetro apropriado do bo
Ar escoa a alta velocidade por um medidor venturi Herchel monitorado por um manômetro de mercúrio, conforme mostrado abaixo. As condições a montante são 150 kPa e 80°C. Se h = 37 cm, estime a vazão em
Deseja-se medir um escoamento de gasolina a 20°C em um tubo de 12 cm de diâmetro, usando um bocal Venturi moderno. Para que os padrões internacionais sejam válidos (figura 6.43), qual é a gama admissí
Um bocal venturi moderno é calibrado em um escoamento de laboratório com água a 20°C. O diâmetro do tubo é 5,5 cm, e o diâmetro da garganta do venturi é 3,5 cm. A vazão é medida por meio de um tanque
Dois reservatórios contendo água, cada qual com área da base de 929 m², estão conectados por um bocal de raio longo de 13 mm de diâmetro, como na figura abaixo. Se h = 30,5 cm , como mostrado para t =