Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 32

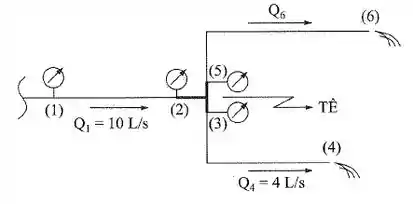
No trecho da instalação da figura, que está num plano horizontal, determinar:

a) a leitura no manômetro (2) para que se possa considerar a perda de carga desprezível no TÊ;

b) a perda de carga de (1) a (2), (5) a (6) e (3) a (4);

c) a potência dissipada em todo o conjunto em kW.

Dados: γ = 10 4   N / m 3 ; p 1 = 0,2 M P a ; p 3 = 0,15   M P a ; p 5 = 0,1   M P a ; A = 10 c m 2 (área da seção das tubulações).

Passo 1

Conforme podemos ver na figura, a vazão total em 1 se divide em 6 e 4, de maneira que podemos escrever:

Q 1 = Q 4 + Q 6 → Q 6 = Q 1 - Q 4 = 0,01 - 0,004 → Q 6 = 0,006   m 3 / s

Agora vamos calcular as velocidades nos potos 2, 3 e 5 através da vazão:

Q 1 = v 2 A → v 2 = Q 1 A = 0,01 10.10 - 4 → v 2 = 10   m / s

Q 4 = v 3 A → v 3 = Q 4 A = 0,004 10.10 - 4 → v 3 = 4   m / s

Q 6 = v 5 A → v 5 = Q 6 A = 0,006 10.10 - 4 → v 5 = 6   m / s

Agora vamos calcular as cargas nos mesmos pontos:

H 2 = v 2 2 2 g + p 2 γ + z 2 = 10 2 2 ( 10 ) + p 2 10 4 + 0 → H 2 = 5 + p 2 10 4

H 3 = v 3 2 2 g + p 3 γ + z 3 = 4 2 2 ( 10 ) + 0,15.10 6 10 4 + 0 → H 3 = 15,8   m

H 5 = v 5 2 2 g + p 5 γ + z 5 = 6 2 2 ( 10 ) + 0,1.10 6 10 4 + 0 → H 5 = 11,8   m

Passo 2

Agora vamos usar o princípio da conservação da energia para o sistema, assim, temos:

γ Q 2 H 2 = γ Q 3 H 3 + γ Q 5 H 5

Agora vamos substituir os valores conhecidos na equação:

10 4 0,01 5 + p 2 10 4 = 10 4 0,004 15,8 + 10 4 0,006 11,8

5 + p 2 10 4 = 13,4 → p 2 = 84000   P a → p 2 = 84   k P a

Passo 3

Agora para a letra b) vamos olhar para o equilíbrio de cargas entre os pontos 1 e 2 para descobrir a perda de carga nesse trecho:

H 1 = H 2 + H p 1,2

v 1 2 2 g + p 1 γ + z 1 = v 2 2 2 g + p 2 γ + z 2 + H p 1,2

Subsituindo os valores conhecidos, temos:

10 2 2 10 + 0,2.10 6 10 4 + 0 = 10 2 2 10 + 84.10 3 10 4 + 0 + H p 1,2 → H p 1,2 = 11,6   m

Agora, da mesma forma, para os pontos 5 e 6:

H 5 = H 6 + H p 5,6

v 5 2 2 g + p 5 γ + z 5 = v 6 2 2 g + p 6 γ + z 6 + H p 5,6

Subsituindo os valores conhecidos, temos:

6 2 2 10 + 0,1.10 6 10 4 + 0 = 6 2 2 10 + 0 10 4 + 0 + H p 5,6 → H p 5,6 = 10   m

Agora, da mesma forma, para os pontos 3 e 4:

H 3 = H 4 + H p 3,4

v 3 2 2 g + p 3 γ + z 3 = v 4 2 2 g + p 4 γ + z 4 + H p 3,4

Subsituindo os valores conhecidos, temos:

4 2 2 10 + 0,15.10 6 10 4 + 0 = 4 2 2 10 + 0 10 4 + 0 + H p 3,4 → H p 3,4 = 15   m

Passo 4

Agora, para encontrar a potência dissipada no conjunto, sabemos que a energia dissipada é fruto das perdas de carga, então podemos escrever:

N d i s s i p a d a = γ Q 1 H p 1,2 + γ Q 4 H p 3,4 + γ Q 6 H p 5,6

Substituindo os valores conhecidos, temos:

N d i s s i p a d a = 10 4 0,01 11,6 + 10 4 0,004 15 + 10 4 0,006 10

N d i s s i p a d a = 2360   W → N d i s s i p a d a = 2,36   k W

Resposta

p 2 = 84   k P a

H p 1,2 = 11,6   m ;   H p 5,6 = 10   m ;   H p 3,4 = 15   m

N d i s s i p a d a = 2,36   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por razões técnicas, pela bomba da instalação da figura devem passar sempre 50L / s . A bomba fornece água ( γ = 10 4 N / m 3 ) aos tanques de grandes dimensões 1 e 2 , com vazões, respectivamente: Q
No processo de produção de um gás líquido, o gás entra pela tubulação 1 A 1 = 0,8m 2 com P 1 = 100k P aa b s , T 1 = 30° C , velocidade média na seção de 70m / s e passa por um compressor e um resfria
Cite quatro quantidade físicas que são conservadas e duas quantidades que não são conservadas durante um processo.
Quando o escoamento através de um volume de controle é em regime permanente?
Defina as vazões de massa e de volume. Como elas estão relacionadas entre si?