Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 153

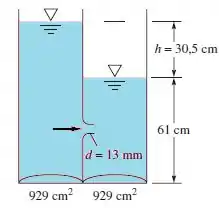
Dois reservatórios contendo água, cada qual com área da base de 929 m², estão conectados por um bocal de raio longo de 13 mm de diâmetro, como na figura abaixo. Se h = 30,5 cm , como mostrado para t = 0, calcule o tempo para h(t) baixar para 7,6 cm.

Passo 1

E aí, gente!! Tudo bem? Vamos para mais um problema de mecânica dos fluidos pra gente resolver juntos!!!

Bem, antes de mais nada vamos catar as propriedades da água a 20°C!!

ρ = 998 k g m 3

μ = 0,001 k g m . s

Para um bocal de raio longo, a gente costuma sempre aproximar β = 0 e chutar um valor inicial para C d = 0,98 ! Para um bocal com β = 0 , a gente vai obter que K p e r d a = 0,9 , observe no gráfico acima!!

Passo 2

A diferença de elevação h deve balancear perdas de carga no bocal e na saída submergido

Δ z = ∑ h p e r d a s = V t 2 2 g ∑ K = V t 2 2 9,81 0,9 b o c a l + 1 s a í d a = h = 0,0968 V t 2 = h

V t 2 = 10,33 h

V t = 3,21 h

Passo 3

Bem, precisamos calcular qual será a vazão que sai pelo orifício?

Q = V t π 4 0,013 2 = 3,21 π 4 0,013 2 = 0,00042 h

Note que no nosso sistema não tem nada “entrando” nele, apenas saindo, ou seja, no nosso balanço de massa a gente tem:

Q e - Q s = Q a c u m u l a d o

Q s a i = - Q a c u m u l a d o = - d v t a n q u e d t

Q s a i = - 1 2 A t a n q u e d h d t

Note que o fator (1/2) que colocamos está pelo fato que, enquanto o tanque da esquerda decresce de acordo com dh, o tanque direito sobe na MESMA quantidade.

Note que nosso Q s a i = Q

Passo 4

Vamos agora fazer a separação de variáveis igualando as equações que encontramos.

0,00042 h = - 1 2 A t a n q u e d h d t

0,00042 2 0,0929 d t = d h h

0,00904 t f i n a l = ∫ 7,6 30,5 d h h → t f i n a l = 2 30,5 - 7,6 0,00904 = 63   s

Resposta

t = 63   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Querosene a 20°C escoa a 18 m³/h em um tubo de 5 cm de diâmetro. Se for instalado um medidor do tipo placa de orifício de 2 cm de diâmetro, com tomadas de pressão de canto, qual será a queda de pressã
Para a combinação de tubo de Pitot e tomada de pressão estática (tubo de Pitot estático) na figura abaixo, o líquido manométrico é água (colorida) a 20°C. Calcule (a) a velocidade na linha de centro,
O reservatório de 1 m de diâmetro na figura abaixo está inicialmente cheio de gasolina a 20°C. Existe um orifício de 2 cm de diâmetro no fundo. Se o orifício é aberto repentinamente, calcule o tempo p
A ducha da figura abaixo libera água a 50°C. Um redutor de vazão do tipo orifício deve ser instalado. A pressão a montante é constante a 400 kPa. Que vazão, em L/min, ocorre sem o redutor? Qual o diâm
Em uma experiência de laboratório, ar a 20°C escoa de um grande tanque por um tubo liso de 2 cm de diâmetro e descarrega na atmosfera ao nível do mar, como mostra a figura abaixo. A vazão é medida por