Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 6.Problemas - Ex. 65

Uma camada de água, com 1   m m de espessura, sobre uma placa eletricamente aquecida é mantida a uma temperatura de T a = 340   K , enquanto ar seco a T ∞ = 300   K escoa sobre a sua superfície (caso A). O conjunto é circundado por uma grande vizinhança que também está a 300   K .

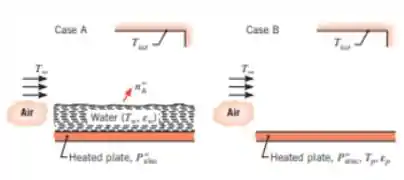
(a) Se o fluxo de evaporação na superfície da água para o ar for de n A ' ' = 0,0 28   k g / ( s · m 2 ) , qual é o valor correspondente do coeficiente de transferência de massa por convecção? Quanto tempo levará para a água evaporar completamente?

(b) Quais são os valores correspondentes do coeficiente de transferência de calor por convecção e da taxa na qual a potência elétrica deve ser fornecida, por unidade de área da placa, para manter a temperatura especificada da água? A emissividade da água é ε a = 0,9 6 .

(c) Se a potência elétrica determinada na parte (b) for mantida após a completa evaporação da água (caso B), qual é a temperatura resultante da placa, cuja emissividade é ε p = 0,60 ?

Passo 1

E aí galerinha, tudo bem?

Vem comigo e juntos vamos resolver essa questão!

Letra a)

Sabemos que o ar está seco ( ρ A , ∞ = 0 ) e que água está a T a = 340   K pelas Tabelas A.6 e A.8:

v A = 5,74   m 3 / k g

ρ = 979,43   k g / m 3

Calculando o coeficiente de transferência de massa por convecção:

n A ' ' = h - m ( ρ A , s - ρ A , ∞ )

n A ' ' = h - m 1 v A - ρ A , ∞

Substituindo os dados:

0,028 = h - m 1 5,74 - 0

h - m = 0,161   m / s

Calculando o tempo que levará para a água evaporar completamente:

n A ' ' = m A A t

n A ' ' = ρ V A t

n A ' ' = ρ A L A t

n A ' ' = ρ L t

Substituindo os dados:

0,028 = 979,43 ⋅ 0,001 t

t = 35   s

Passo 2

Letra b)

Para determinarmos o coeficiente de transferência de calor, teremos que aplicar a analogia de Reynolds:

h h m = ρ c p L e 2 3

Calculando a temperatura de filme:

T f = T s - T ∞ 2 = 300 + 340 2 = 320   K

Pelas Tabelas A.4 e A.8, obtemos:

k = 0,028   W / m ⋅ K

ρ = 1,08   k g / m 3

c p = 1008   J / k g ⋅ K

D A B 298   K = 0,26 × 10 - 4   m 2 / s

Agora, obtemos a difusividade para a temperatura de filme:

D A B 1 D A B 2 = T 1 T 2 3 2

0,26 × 10 - 4 D A B 2 = 298 320 3 2

D A B 2 = 0,29 × 10 - 4   m 2 / s

Passo 3

Calculando o número de Lewis:

L e = k ρ c p D B

Substituindo os dados do Passo 2:

L e = 0,028 1,08 ⋅ 1008 ⋅ ( 0,29 × 10 - 4 )

L e = 0,889

Calculando h pela analogia de Reynolds:

h 0,161 = 1,08 ⋅ 1008 ⋅ 0,889 2 3

h = 162   W / m 2 ⋅ K

Passo 4

Aplicando um balanço de energia para o sistema:

d E d t = E ˙ e n t - E ˙ s a i + E ˙ g

E ˙ e n t = E ˙ s a i

Abrindo essa equação:

P e l e ' ' = q c o n v ' ' + q e v a p ' ' + q r a d ' '

P e l e ' ' = h T s - T ∞ + n A ' ' ∆ H e v a p + ε σ T s 4 - T ∞ 4

Pela Tabela A.6 a T a = 340   K , temos:

∆ H e v a p = 2342   k J / k g

Substituindo os dados:

P e l e ' ' = 162 ⋅ 340 - 300 + 0,028 ⋅ 2342 × 10 3 + 0,96 ⋅ 5,67 × 10 - 8 ⋅ ( 340 4 - 300 4 )

P e l e ' ' = 72342,5   W / m 2

Passo 5

Letra c)

Aplicando um balanço de energia:

d E d t = E ˙ e n t - E ˙ s a i + E ˙ g

E ˙ e n t = E ˙ s a i

Abrindo essa equação:

P e l e ' ' = q c o n v ' ' + q r a d ' '

P e l e ' ' = h T p - T ∞ + ε σ T p 4 - T ∞ 4

Substituindo os dados encontramos a temperatura resultante da placa:

72342,5   = 162 ⋅ T p - 300 + 0,6 ⋅ 5,67 × 10 - 8 ⋅ T p 4 - 300 4

162 T p + 3,402 × 10 - 8 T p 4 - 121218 = 0

T p = 748,2   K = 475,2 ° C

Ufa! Acabamos a nossa questão!

Até a próxima!

Resposta

a )   h - m = 0,161   m / s   e   t = 35   s

b )   h = 162   W / m 2 ⋅ K   e   P e l e ' ' = 72342,5   W / m 2

c )   T p = 748,2   K = 475,2 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Células a combustível similares à célula MPT do Exemplo 1.5 operam com uma mistura de água líquida e metanol ao invés de hidrogênio; o ânodo é colocado em contato direto com o combustível líquido. Oxi
Refaça os exercícios (2) e (3) na situação em que escoa sobre:a) uma esfera de 0,1c m de diâmetro.b) uma cápsula cilíndrica de 0,1c m de diâmetro.
Proponha um algoritmo semelhante ao descrito pelas equações 9.90 , utilizando-se o integrador tipo Runge-Kutta-Gill.
Qual a importância do número de Schmidt no estudo da convecção mássica natural?
Demonstre as equações 9.66 ,9.67e( 9.91 )