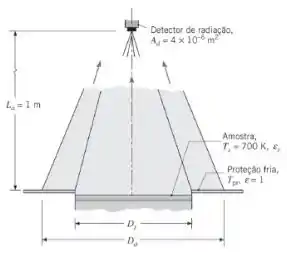
Um detector de radiação, que tem uma área sensível , está configurado para receber a radiação de uma área alvo com diâmetro , quando localizado a uma distância do alvo. Para o dispositivo experimental mostrado na figura, desejamos determinar a radiação emitida por uma amostra aquecida com diâmetro . A temperatura da amostra de alumínio é de e sua emissividade é . Uma proteção fria na forma de um anel é colocada nas laterais da amostra para minimizar o efeito da radiação que vem de fora da área da amostra; contudo, ela ocupa parte da área alvo. A amostra e a proteção fria são emissores difusos.

(a) Admitindo que a proteção seja negra, em qual temperatura, , a proteção deve ser mantida para que a radiação emitida por ela seja da taxa de energia radiante total recebida pelo detector?

(b) Sujeito à restrição paramétrica de que a radiação emitida pela proteção deva ser de ou da radiação total recebida pelo detector, represente graficamente a temperatura da proteção, , requerida para satisfazer essas condições como uma função da emissividade da amostra para

Para resolver essa questão vamos assumir que:

(1) A amostra é difusa e cinza;

(2) A blindagem fria é preta;

(3) .

A potência radiante interceptada pelo detector de dentro da área alvo é,

A contribuição da amostra é,

A contribuição da blindagem fria em forma de anel é:

E, a partir da geometria do detector de blindagem,

Onde,

Temos que,

Onde,

O requisito de que a radiação emitida pela blindagem fria seja da radiação total interceptada pelo detector é expresso como,

Avaliando essa equação com a do Passo 1, encontramos: