Uma central de transmissão de uma malha de instrumentação é uma caixa, com circuitos eletrônicos e uma fonte de energia para enviar os sinais dos sensores até uma unidade receptora, onde é feito o registro dos dados. Uma central desta é colocada sobre um sistema de correias transportadoras, que passa através de um grande forno de solda a vácuo, como mostrado na figura. As superfícies expostas da caixa têm um revestimento especial, opaco e difuso, cuja emissividade espectral é também mostrada na figura.

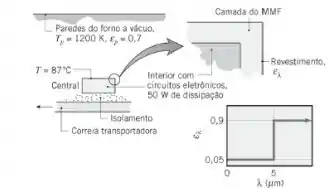
Para estabilizar a temperatura da central e prevenir o superaquecimento dos componentes eletrônicos, a superfície interna da caixa é coberta por uma camada de um material que muda de fase (MMF), com uma temperatura de fusão de e um calor de fusão de . A central tem uma área de superfície exposta igual a , enquanto a massa do MMF é de . Além disso, sabe-se que a potência dissipada pelos componentes eletrônicos é de . Considere uma situação na qual a central entra no forno a uma temperatura uniforme de e todo o MMF se encontra no estado sólido. Quanto tempo será necessário para que todo o MMF passe para o estado líquido?

Para resolver essa questão vamos assumir:

(1) Área da superfície das paredes do forno muito maior que a do casulo;

(2) Nenhuma convecção;

(3) Nenhuma transferência de calor para o casulo do transportador;

(4) O revestimento do casulo é difuso, opaco;

(5) Inicialmente a temperatura interna do casulo é uniforme em e permanece assim durante o intervalo de tempo ;

(6) A área de superfície fornecida é a que está exposta às paredes.

Fazendo um balanço de energia na caixa por um intervalo de tempo que corresponde ao tempo em que o PCM muda do estado sólido para o líquido,

Onde é a taxa de dissipação de energia elétrica, é a massa do PCM e hfg é o calor da fusão do PCM.

A irradiação é:

Já a força emissiva é:

E a emissividade:

Onde, da Tabela 12.1, com .

A absortividade, , é:

Onde, da Tabela 12.1, com .

Substituindo os valores numéricos no balanço energético, encontramos,