Um procedimento para medir a condutividade térmica de sólidos a temperaturas elevadas envolve a colocação de uma amostra na base de um grande forno. A amostra tem uma espessura e é colocada no interior de um recipiente quadrado de lado . As laterais são termicamente isoladas. As paredes da cavidade são mantidas a , enquanto a superfície inferior da amostra é mantida a uma temperatura muito mais baixa pela circulação de um refrigerante através do recipiente que contém a amostra. A superfície da amostra é difusa e cinza, com uma emissividade . Sua temperatura é medida oticamente.

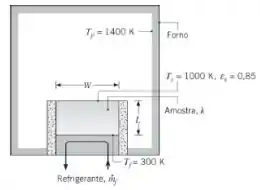
(a) Desprezando efeitos convectivos, obtenha uma expressão pela qual a condutividade térmica da amostra possa ser avaliada em termos de grandeza medidas e conhecidas As medições são feitas em condições de regime estacionário. Sendo e , qual é a condutividade térmica da amostra?

(b) Se e o refrigerante for água a uma vazão de , é razoável admitir uma temperatura uniforme na superfície inferior da amostra?

Para resolver essa questão vamos assumir:

(1) Condições em estado estacionário;

(2) Condução unidimensional na amostra;

(3) Constante

(4) Superfície cinza-difusa;

(5) Irradiação igual à emissão do corpo negro a .

Do balanço de energia na superfície superior temos,

Onde,

Então,

Resolvendo a condutividade térmica e substituindo valores numéricos, encontramos,

Substituindo os valores,

A não uniformidade da temperatura da superfície inferior depende do aumento da temperatura do líquido de refrigeração. Então do balanço energético,

Substituindo os valores,

A variação em é pequena em comparação com Portanto, não é grande o suficiente para introduzir um erro significativo na determinação de .