Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 77
77 – Ar deve ser aquecido passando através de um banco de tubos de de comprimento no interior onde ocorre condensação de vapor a . O ar aproxima-se do banco de tubos na direção normal a e , a uma velocidade média de . O diâmetro externo dos tubos é , e estes estão dispostos em um arranjo escalonado com passos longitudinal e transversal de . Há 20 fileiras na direção do escoamento com 10 tubos em cada uma. Determine (a) a taxa de transferência de calor, (b) a queda de pressão através do banco de tubos e (c) a taxa de condensação do vapor no interior dos tubos.
Passo 1
Dados fornecidos:
Temperatura do ar,
Pressão do ar,
Velocidade média do fluxo de ar,
Comprimento dos tubos,
Diâmetro externo do tubo,
Temperatura de condensação do vapor,
Número de linhas dos tubos,
Número de tubos em cada linha,
Passo longitudinal,
Passo transversal,
Passo 2
A vista em corte transversal da disposição dos tubos é mostrada abaixo:
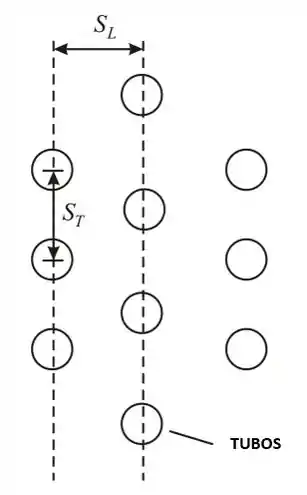
Passo 3
Com a pressão de e assumindo a temperatura média do ar como , temos:
O número Prandtl é:
Condutividade térmica é:
A viscosidade dinamica é:
Calor específico de:
Densidade:
Com a temperatura de :
O número Prandtl é:
Com a temperatura de :
Passo 4
A velocidade máxima do fluxo é determinada a partir da equação dada por:
Passo 5
Como o número de Reynolds é determinado a partir da equação dada por:
O número de Nusselt é determinado a partir da equação dada por:
Como , o número de Nusselt médio é dado por:
O coeficiente convectivo de transferência de calor do ar é determinado a partir da equação dada por:
Reescreva para achar :
Passo 6
O número total de tubos é determinado como:
A área da superfície de transferência de calor por unidade de comprimento do tubo é determinada como:
A vazão mássica do ar é determinada como:
Passo 7
A temperatura de saída do ar é determinada a partir da expressão dada por:
A diferença logarítmica da temperatura média do ar é determinada a partir da equação dada por:
Passo 8
- A taxa de transferência de calor por unidade de comprimento do tubo é determinada a partir da equação dada por:
- O fator de atrito e o fator de correção para o fluxo são determinados como
- Das propriedades do lençol freático em , temos .
A taxa de transferência de calor por unidade de comprimento é .
Passo 9
A partir da figura, fator de atrito e fator de correção para espaços em branco do tubo
Para arranjo escalonado:
Em e
Fator de atrito,
Fator de correção,
A queda de pressão através do banco de tubos é obtida a partir da equação dada por:
A queda de pressão no banco de tubos é
Passo 10
A taxa de condensação do vapor no interior dos tubos é determinada como:
A taxa de condensação do vapor no interior dos tubos é .
Resposta
- A taxa de transferência de calor por unidade de comprimento é .
- A queda de pressão no banco de tubos é
- A taxa de condensação do vapor no interior dos tubos é .