Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 164
Um esquema para aquecer simultaneamente correntes separadas de água e de ar envolve a sua passagem através e sobre um conjunto de tubos, respectivamente, enquanto as paredes dos tubos são aquecidas eletricamente. Para aumentar a transferência de calor no lado do gás, aletas anulares de perfil retangular são fixadas à superfície externa dos tubos. A fixação é facilitada pelo uso de um adesivo dielétrico, que isola eletricamente as aletas da parede do tubo por onde passa a corrente elétrica.
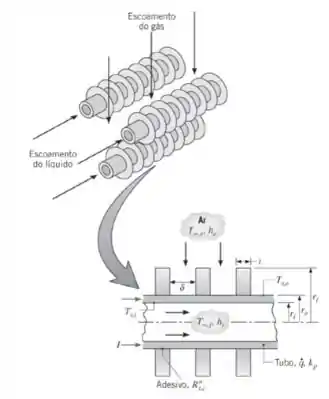
- Supondo geração de calor volumétrica uniforme no interior da parede do tubo, obtenha expressões para as taxas de transferência de calor, por unidade de comprimento do tubo (), nas suas superfícies interna () e externa (). Expresse os seus resultados em termos das temperaturas nas superfícies interna e externa do tubo, e , e de outros parâmetros pertinentes.
- Obtenha expressões que possam ser usadas para determinar e em termos dos parâmetros associados às condições nos lados da água e do ar.
- Considere condições nas quais a água e o ar estão a , com coeficientes de transferência de calor correspondentes de e . O calor é uniformemente dissipado no tubo de aço inoxidável (), com raios interno e externo e , e aletas de alumínio (, ) fixadas na sua superfície externa com . Determine as taxas de transferência de calor e as temperaturas nas superfícies interna e externa do tubo em função da taxa volumétrica de aquecimento . O limite superior para será determinado pelas restrições de que não pode exceder o ponto de ebulição da água () e não deve exceder a temperatura de decomposição do adesivo ().
Passo 1
Opa! Fala aí! Vamos matar essa questãozinha show de bola? Vamos sim!
Ela parece bem grande e assustadora, né?
Mas não é nada disso! Relaxa que a gente dá conta junto!
Temos três letrinhas para resolver… Vamos começar pelo começo!
A letra a, pede pra gente encontrar as expressões para as taxas de transferência de calor que sejam em função das temperaturas… Hummm… Pra isso vamos usar a equação C.8 do apêndice C do livro, ela nos mostra o seguinte:
Agora vamos substituir nossos termos nela, ok?
Primeiro para a equação em , e depois em :
Show de bola! Não esqueça que a gente tirou o por que nosso enunciado pediu a transferência de calor por unidade de comprimento do tubo, beleza?
Passo 2
Letra b agora!
Ele quer que a gente encontre as expressões que determinam e , vamos nessa então!
Vamos ter que ir de novo lá no apêndice C, beleza? E pegar as equações que descrevem o equilíbrio de energia da superfície interna e da externa… São as equações C.16 e C.17:
Agora vamos substituir nossos termos nas dua equações, certo?
Tranquilo? Agora só falta a nossa letra c!
Passo 3
Bom, a letra c quer que a gente encontre as taxas de transferência de calor e as temperaturas nas superfícies interna e externa do tubo… Mas ele faz uma série de considerações… Humm… Vamos anotar elas aqui embaixo pra gente não esquecer quais são elas, beleza?
Usando os limites de temperatura e , vamos encontrar o que ele quer nas equações da letra a e da letra b, vamos nessa então:
Agora vamos fazer o mesmo para a temperatura:
E pra fechar:
Prontinho! Conseguimos!
Resposta
- ;
;