Um fio comprido de constantan, com 1 mm de diâmetro, tem uma de suas extremidades soldada à superfície de um grande bloco de cobre, formando uma junção de termopar. O fio se comporta como uma aleta, permitindo a saída de calor da superfície e, assim, diminuindo a temperatura medida na junção Tj em relação à temperatura do bloco, To.
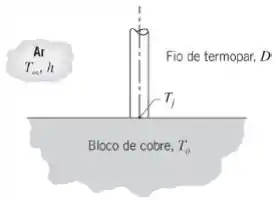
(a) Se o fio encontra-se no ar a , com um coeficiente convectivo de estime o erro de medida do termopar quando o bloco estiver a .
(b) Para coeficientes de transferência de calor por convecção de e represente graficamente o erro de medida em função da condutividade térmica do material do bloco na faixa de a. Sob quais circunstâncias é vantajoso utilizar um fio com menor diâmetro?
Passo 1
Nessa questão nós temos um fio longo e constante, soldado a um grande bloco de cobre, formando uma junção de termopar na superfície do bloco. E com isso queremos encontrar o erro de medição para o termopar para as condições prescritas.
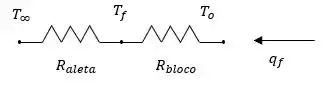
Para esse esquema, temos que o circuito térmico é:
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições de estado estacionário;
(2) O fio do termopar se comporta como uma aleta com coeficiente de transferência de calor constante;
(3) O bloco de cobre tem temperatura uniforme, exceto nas proximidades da junção.
O fio do termopar se comporta como uma aleta longa, permitindo que o calor flua da superfície, diminuindo assim a temperatura da junção de detecção abaixo da do bloco, .
No bloco, o calor flui para a região circular da interface bloco-arame e a resistência térmica ao fluxo de calor dentro do bloco é aproximada como um disco de diâmetro em um meio semi-infinito
Passo 3
A combinação termopar-bloco pode ser representada por um circuito térmico, como mostrado no Passo 1. Onde a resistência térmica da aleta segue a expressão da taxa de calor para uma aleta infinita,
O fator de forma para o disco em um meio semi-infinito é dado como e, portanto,
Do circuito térmico,
Passo 4
Com,
e
E as resistências térmicas,
Substituindo os valores,