Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 151
Devido ao grande número de componentes nos chips dos PCs atuais, dissipadores de calor aletados são usados com frequência para manter o chip a uma temperatura de operação aceitável. Dois projetos de dissipadores aletados devem ser avaliados, ambos com a área da base (sem aletas) de dimensões . As aletas possuem seção reta quadrada e são fabricadas em uma liga de alumínio extrudada com uma condutividade térmica de Ar de resfriamento pode ser fornecido a e a temperatura máxima permissível do chip é de . Outras características do projeto e condições operacionais são apresentadas na tabela a seguir.
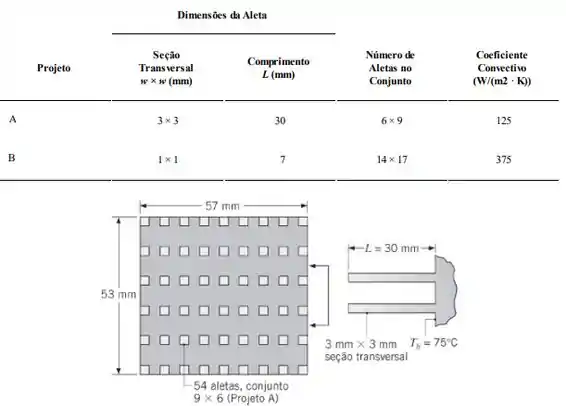
Determine o melhor arranjo de aletas. Na sua análise, calcule a taxa de transferência de calor, a eficiência e a efetividade de uma única aleta, bem como a taxa total de transferência de calor e a eficiência global do conjunto de aletas. Uma vez que o espaço disponível no interior de um computador é importante, compare a taxa total de transferência de calor por unidade de volume para os dois projetos.
Passo 1
Nessa questão, nós temos dois dissipadores de calor com aletas, modelos A e B, com o número de aletas na matriz, , dimensões das aletas de seção quadrada, e comprimento, , com diferentes coeficientes de convecção, .
E nós queremos determinar qual arranjo das aletas é superior. Além de calcular a taxa de aquecimento, , eficiência, e efetividade,, de uma única aleta, bem como a taxa de calor total, e a eficiência global, , da matriz. Além disso, devemos comparar as taxas totais de calor por unidade de volume.
Passo 2
Para resolver esse problema, precisamos assumir que:
(1) Estamos em condições de estado estacionário;
(2) A condução é unidimensional nas aletas;
(3) O coeficiente de convecção é uniforme sobre a aleta e superfície;
4) As pontas de aleta sofrem convecção;
(5) As propriedades são constantes.
A eficiência global da matriz:
Onde é a área total da superfície, a soma da parte exposta da base (área principal) mais as superfícies das aletas, que pode ser escrita por:
Onde a área de superfície de uma única aleta e a área principal são:
Passo 3
Combinando a equação da eficiência global com a da área total, chegamos em:
Onde é a eficiência de uma única aleta. No Caso A, para a condição de ponta com convecção, a eficiência de uma única aleta única é:
Onde,
Passo 4
A efetividade de uma única aleta, é:
Além disso, queremos comparar o desempenho dos projetos em relação ao volume da matriz. Onde,
Resolvendo as equações substituindo os valores numéricos apropriados, os resultados são:
Ambos os projetos têm boas eficiências e efetividades. Claramente, o Projeto B é superior porque a taxa de aquecimento é quase maior que o Projeto A para a mesma pegada de placa. Além disso, o espaço necessário para o Projeto B é quatro vezes menor e a taxa de aquecimento por unidade de volume é vezes maior.
Resposta
