Um fogão a lenha é equipado com um queimador superior para cozimento. O queimador, com diâmetro , é fabricado em ferro fundido O lado inferior (combustão) do queimador tem aletas planas de seção transversal uniforme, montadas como mostrado no esquema. Um revestimento muito fino de cerâmica encontra-se sobre todas as superfícies do queimador. A parte superior do queimador está exposta às condições do ambiente externo enquanto a parte inferior do queimador está exposta às condições de combustão Compare a temperatura na superfície superior do queimador aletado àquela que estaria presente para um queimador sem aletas. Sugestão: Use a mesma expressão para a transferência de calor por radiação para a parte inferior do queimador aletado e para o queimador sem aletas.
Passo 1
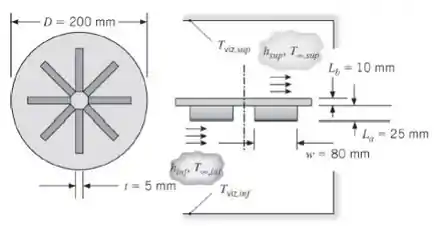
Nessa questão nós temos a geometria de um queimador de ferro fundido com e sem aletas. Além da temperatura ambiente, temperatura de combustão, coeficiente de transferência de calor na superfície superior do queimador, coeficiente de transferência de calor na superfície inferior do queimador, emissividade do revestimento do queimador e condutividade térmica do ferro fundido.
Muita coisa, eu sei, mas vamos com calma. Aqui nós queremos encontrar a temperatura da superfície superior do queimador com e sem aletas, ta bem? Então vamos para as nossas considerações.
Passo 2
Para resolver essa questão vamos assumir que:
(1) Estamos em condições unidimensionais e em estado estacionário;
(2) As propriedades são constantes;
(3) Convecção da ponta da aleta;
(4) Ampla área na parte superior e inferior do queimador.
Avaliando a transferência de calor por radiação dos produtos de combustão para o fundo do queimador como:
Temos que a transferência total de calor para o fundo da base do queimador é:
Onde,
Passo 3
A transferência total de calor da superfície superior é:
A condução unidimensional através da base do queimador é:
No estado estacionário, as taxas de calor devem ser iguais.
;
A eficiência da aleta pode ser avaliada usando a Tabela 3.5 e o comprimento da aleta corrigido é:
A área da aleta é:
E o valor de é:
E finalmente, temos que a eficiência é:
Passo 4
Substituindo os valores encontrados nas equações do Passo 2, encontramos:
Para um queimador sem aletas, temos:
Substituindo os valores, encontramos:
Resposta
Com aleta:
Sem aleta: