Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 168
Que diâmetro deve ser empregado em um tubo de água para gerar 0,075 a uma perda de carga de 500 kPa? O comprimento do tubo é 175 m e a sua rugosidade é 2,5 mm.
Passo 1
Oi pessoal, tudo bem ?
Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga (ou equação da energia):
Consideremos:
;
;
As perdas de carga serão representadas pela eq da perda de carga maior, a eq perda de carga menor será desprezada:
Passo 2
Do problema, temos:
Obs: propriedades da água à , Tabela A.7 .
Façamos a análise do primeiro tubo: Assim, a equação da energia, de forma simplificada, fica:
Porém, da eq 1, não sabemos o valor da velocidade, mas sabemos a vazão:
Substituindo as expressões na equação 1:
Isolando o D, temos:
Sabe-se também que o Re é dado por:
E que:
Passo 3
A equação 1 é complicada porque D é desconhecido, portanto V é desconhecido (mesmo que Q seja conhecido), e Re e, portanto, f são desconhecidos! Podemos configurar o Excel para resolver a Eq 1, o número de Reynolds e f, simultaneamente, variando D:
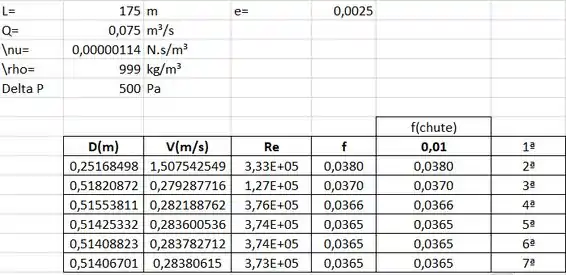
Observe que, a partir da 6ª iteração, os valores começam a se repetir, então inclinam-se para a convergência.
Resposta
Portanto, o diâmetro a ser empregado é de