Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 193

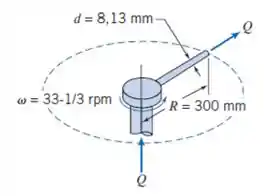
Um dispositivo simples de irrigação gira com velocidade angular constante, conforme mostrado. Água é bombeada através do tubo com uma vazão Q = 13,8   L / m i n . Determine o torque que deve ser aplicado para manter o dispositivo com rotação constante usando dois métodos de análise:

a) Um volume de controle rotativo;

b) Um volume de controle fixo.

Passo 1

Equação:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Estacionário;
  3. Cancelamento do torque no corpo;
  4. F S = 0 ;
  5. Não há k ^ na aceleração centrípeta;
  6. ω - = 0 ;
  7. r × V = 0 .

Passo 2

Letra a)

Determinando o torque que deve ser aplicado para manter o dispositivo com rotação constante usando um volume de controle rotativo.

Realizando as considerações apresentadas no Passo 1, temos:

T e i x o - ∫ V C r × 2 ω × V ρ d ∀ = 0

T e i x o = ∫ V C r × 2 ω × V ρ d ∀

T e i x o = 2 ω V ρ A ∫ 0 R r d r

Integrando:

T e i x o = ω V ρ A R 2

Sendo V ⋅ A = Q :

T e i x o = ω ρ Q R 2

Passo 3

Calculando T e i x o :

Sendo:

ρ = 1000   k g / m 3 ;

Q = 1 3 , 8   L / m i n = 2 , 3 x 10 - 4   m 3 / s ;

ω = 33 1 3   r p m = 100 3 ⋅ 2 π 60 = 3,49   r a d / s ;

R = 300   m m = 0,3   m .

Temos:

T e i x o = 3,49 ⋅ 1000 ⋅ 2,3 x 10 - 4 ⋅ 0,3 2 = 0,072   N ⋅ m

Passo 4

Letra b)

Determinando o torque que deve ser aplicado para manter o dispositivo com rotação constante usando um volume de controle fixo.

T e i x o = ∫ S C r × V   ρ V d A

Em relação às coordenadas fixas x y :

r = r cos ⁡ θ î + s e n   θ j ^

V = V cos ⁡ θ î + s e n   θ j ^ + r ω ( - s e n   θ   î + cos ⁡ θ j ^ )

Então:

r × V = i j k r cos ⁡ θ r   s e n   θ 0 v cos ⁡ θ - r ω   s e n   θ v   s e n   θ + r ω cos ⁡ θ 0

r × V = r cos ⁡ θ v   s e n   θ + r ω cos ⁡ θ - r   s e n   θ v cos ⁡ θ - r ω   s e n   θ k ^

r × V = ω r 2 cos 2 ⁡ θ + s e n 2   θ k ^ = ω r 2

Assim, voltando na equação principal:

T e i x o = ∫ S C r × V   ρ V d A = T e i x o = ∫ S C ω R 2 ρ V d A

Integrando:

T e i x o = ω R 2 ρ V A = ω R 2 ρ Q

Passo 5

Calculando T e i x o :

Sendo:

ρ = 1000   k g / m 3 ;

Q = 13,8   L / m i n = 2,3 x 10 - 4   m 3 / s ;

ω = 33 1 3   r p m = 100 3 ⋅ 2 π 60 = 3,49   r a d / s ;

R = 300   m m = 0,3   m .

Temos:

T e i x o = 3,49 ⋅ 1000 ⋅ 2,3 x 10 - 4 ⋅ 0,3 2 = 0,072   N ⋅ m

Os dois métodos produzem o mesmo resultado.

Resposta

T e i x o = 0,072   N ⋅ m

T e i x o = 0,072   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque alto descarrega através de um orifício circular, como na Figura P3.95. Use a fórmula de Torricelli do problema P3.81 para calcular a velocidade de saída. (a) Se, nesse instante, a força F ne
Um jato líquido de massa específica ρ e área A atinge um bloco e se divide em dois jatos, como na Figura P3.75. Considere a mesma velocidade V para os três jatos. O jato superior sai com um ângulo θ e
o carrinho da Figura P3.107 move-se à velocidade constante V 0 = 12m / s e coleta água com uma concha de 90 cm de largura que se aprofunda h = 2,5c m em um lago. Despreze o arrasto do ar e o atrito da
Modifique o Exemplo 3.15, de modo que o braço parta do repouso e acelere até sua velocidade final de rotação. O momento de inércia do braço em relação a O é I o . Desprezando o arrasto do ar, encontre
Aplique o Problema P3.108 ao seguinte caso: M t o t a l = 900k g , b = 60c m ,h = 2c m ,V o = 120m / s , com o foguete do Problema P3.35 ligado e funcionando. Calcule V após 3 s.