Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 75
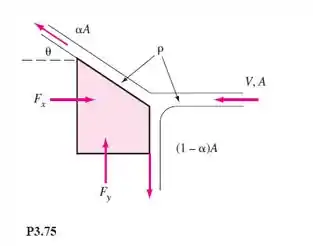
Um jato líquido de massa específica e área A atinge um bloco e se divide em dois jatos, como na Figura P3.75. Considere a mesma velocidade V para os três jatos. O jato superior sai com um ângulo e área . O jato inferior sai a 90° para baixo. Desprezando o peso do fluido, (a) deduza uma fórmula para as forças necessárias para suportar o bloco contra as variações de quantidade de movimento do fluido. (b) Mostre que somente se (c) Encontre os valores de e para os quais tanto como são nulas.
Passo 1
Bora resolver mais essa juntos!
Em (a) queremos uma fórmula para as forças necessárias para suportar o bloco, como podemos ver na Figura 3.75, teremos duas delas, a e a . Pelas expressões de momento, teremos o seguinte:
Cara, note que , considerando o jato de entrada, belê?! Vamos agora rearranjar essas equações, assim:
Passo 2
Beleza, letra (a) já se foi! Bora pra letra (b).
Queremos mostrar que somente se . Cara, analisando a nossa expressão da letra (a) para , teremos sendo zero a partir de:
Mas olha só, isso não faz sentido para , porque não vai zerar! Teremos que , só assim chegaremos em uma .
Passo 3
Já tamo na (c), caraca, foi rápido né?!
Queremos encontrar e para as forças que sustentam o bloco sendo nulas. Analisando as expressões que encontramos na letra (a), vemos que:
Isso ai só vai ser zero se assim, teremos . Isso também é válido para , assim, a única forma das duas serem nulas é no caso de um fluxo horizontal, onde:
Resposta
Ei, a resposta está no passo a passo :)