Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 95

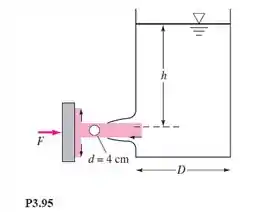
Um tanque alto descarrega através de um orifício circular, como na Figura P3.95. Use a fórmula de Torricelli do problema P3.81 para calcular a velocidade de saída. (a) Se, nesse instante, a força F necessária para segurar a placa for 40 N, qual é a profundidade h? (b) Se a superfície da água no tanque está baixando a uma taxa de 2,5 cm/s, qual é o diâmetro D do tanque?

Passo 1

Vamo lá!

Vamos fazer uma análise de movimento ai, um balanço de forças, assim:

∑ F x = F = - m ˙ e n t r a u e n t r a = - m ˙ j a t o s a i d a - V j a t o s a i d a

Tendo m ˙ = ρ A V , teremos:

∑ F x = F = - m ˙ e n t r a u e n t r a = ρ A o r i f i c i o V j a t o s a i d a V j a t o s a i d a = ρ π 4 d 2 V j a t o s a i d a 2

Por Torricelli teremos que:

V j a t o s a i d a 2 = 2 g h

Assim, substituindo e isolando h, teremos:

h = F ρ π 4 d 2 2 g

Passo 2

Para (a), basta substituirmos as informações oferecidas pelo enunciado e pela figura, assim:

h = 40   N 1000 k g m 3 π 4 0,04   m 2 2 ⋅ 9,81 m s 2 = 1,62   m

Passo 3

Vamo pra (b). Perceba que a altura do tanque vai descer bem pouco, em 1 segundo teremos uma variação de apenas 0,025 m. Assim, vamos trabalhar com uma expressão de vazão média para determinar o diâmetro do tanque.

Inicialmente, vamos tirar uma média da altura no intervalo de 1 s, assim:

h m é d i a = 1,62 + 1,595 2 = 1,6075   m

Daí,

Q m é d i a = A o r i f í c i o V j a t o s a i d a = A o r i f i c i o 2 g h m é d i a = π 4 d 2 2 g h m é d i a

Substituindo os dados:

Q m é d i a = π 4 0,04   m 2 2 9,81 m s 2 1,6075   m ≈ 0,00705   m 3 / s

Assim, temos pela seguinte equação:

Q Δ t = A t a n q u e Δ h = π 4 D 2 Δ h → D = Q Δ t π 4 Δ h = 0,00705 m 3 s ⋅ 1   s π 4 ⋅ 0,025   m = 0,60   m

Resposta

  1. 1,62 m
  2. 0,60 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha expressões para a taxa de variação em massa do volume de controle mostrado, bem, como as forças horizontal e vertical requeridas para manter o volume de controle fixo, em função de P 1 ,A 1 ,V
Calcule a força requerida para manter o tampão fixo na saído do tubo de água. A vazão é 1,5m 3 / s e a pressão a montante é 3,5M P a .
Água está escoando em regime permanente por um cotovelo de 180 ° . Na entrada do cotovelo, a pressão manométrica é 103k P a . A água é descarregada para a atmosfera. Considere que as propriedades são
Em um cotovelo redutor de 180 ° de diâmetro interno de 0,2m , a água tem uma velocidade média de 0,8m / s e uma pressão manométrica de 350k P a . Na saída, a pressão é 75k P a , e o diâmetro é 0,04m .
Água está escoa em regime permanente pelo bocal mostrado, descarregando para a atmosfera. Calcule a componente horizontal da força na junta flangeada. Indique se a junta está sob tração ou compressão.