Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 27

As distribuições espectrais de Wien e de Rayleigh-Jeans são aproximações da lei de Planck para o poder emissivo espectral, que são úteis nos limites inferior e superior do produto λT, respectivamente.

  1. Mostre que a distribuição espectral de Planck terá a forma

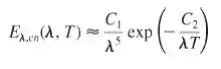
    2. quando C2/(λT) >>1 e determine o erro (em comparação com a distribuição exata) para a condição λT = 2898 μm · K. Essa forma é conhecida por lei de Wien.

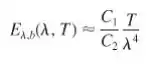
  2. Mostre que a distribuição de Planck assumirá a forma

quando C2/(λT)

Passo 1

Eita! Demos de cara com uma questão de demonstração…

Fica de boa que juntos a gente dá conta, beleza?

Vamos começar pela letra a, pela distribuição de Planck nós podemos usar a equação 12.30, que mostra o seguinte:

E λ ,   b ( λ ,   T ) = C 1 λ 5 . e x p C 2 λ   .   T - 1

Nessa equação se a gente considerar:

C 2 λ   .   T > > 1

E isso quer dizer que:

e x p C 2 λ   .   T > > 1

Então pensa bem, se temos um número muito maior do que um e diminuímos 1, não faz muita diferença, certo?

Vamos ficar então com:

E λ ,   b ( λ ,   T ) ≈ C 1 λ 5 . e x p - C 2 λ   .   T

Passo 2

Agora que nós conseguimos provar, vamos achar o erro que ele pediu também:

E λ ,   b ,   W i e n E λ ,   b ,   P l a n c k = 1 / e x p C 2 λ   .   T 1 / e x p C 2 λ   .   T   - 1

E λ ,   b ,   W i e n E λ ,   b ,   P l a n c k = 1 / e x p 14388 2898 1 / e x p 14388 2898   - 1

E λ ,   b ,   W i e n E λ ,   b ,   P l a n c k = 0,9930

Opa! Olha só nossa aproximação foi muito boa, hein?

Passo 3

Agora na letra b, vamos considerar:

C 2 λ   .   T < < 1

E isso quer dizer que nossa exponencial se aproxima de uma série que pode ser aproximada pelos dois primeiros termos, olha só um exemplo mais simples aqui:

e x = 1 + x + x 2 2 ! + x 3 3 ! + . . .   ≈ 1 + x

Trazendo para a nossa realidade, e usando a aproximação de Rayleigh-Jeans, vamos ficar com o seguinte:

E λ ,   b ( λ ,   T ) ≈ C 1 λ 5 . 1 + C 2 λ   .   T - 1

E λ ,   b ( λ ,   T ) ≈ C 1 C 2   .   T λ 4

Passo 4

Agora que a parte de provar já foi, vamos achar o erro que ele pediu:

E λ ,   b ,   R - J E λ ,   b ,   P l a n c k = C 1 C 2   .   T λ 4 C 1 λ 5 . e x p C 2 λ   .   T - 1

E λ ,   b ,   R - J E λ ,   b ,   P l a n c k = λ   .   T C 2 . e x p C 2 λ   .   T - 1

E λ ,   b ,   R - J E λ ,   b ,   P l a n c k = 100000 14388 . e x p 14388 100000 - 1

E λ ,   b ,   R - J E λ ,   b ,   P l a n c k = 1,0754

Olha vimos que a aproximação de Rayleigh-Jeans também foi boa, né?

Show! Conseguimos terminar!

Resposta

  1. Passo 1 e E λ ,   b ,   W i e n E λ ,   b ,   P l a n c k = 0,9930 .

  2. Passo 3 e E λ ,   b ,   R - J E λ ,   b ,   P l a n c k = 1,0754 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estime o comprimento de onda que corresponde à máxima emissão de cada uma das seguintes superfícies: o Sol, um filamento de tungstênio a 2500 K, um metal aquecido a 1500 K, pele humana a 305 K e uma s
Materiais fotovoltaicos convertem a luz solar diretamente em potência elétrica. Alguns dos fótons que incidem sobre o material deslocam elétrons que são então capturados para criar a corrente elétrica
Admitindo que a superfície da Terra seja negra, estime sua temperatura considerando que o Sol tenha uma temperatura equivalente a de um corpo negro a 5800 K. Os diâmetros do Sol e da Terra são de 1,39
Um elemento aquecedor radiante em forma de um anel é energizado eletricamente e mantido a uma temperatura Ta = 3000 K. O elemento aquecedor é usado em um processo de fabricação para aquecer uma pequen