Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 28

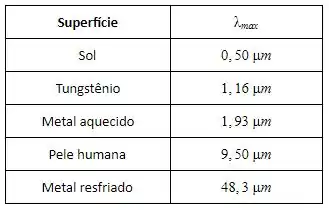
Estime o comprimento de onda que corresponde à máxima emissão de cada uma das seguintes superfícies: o Sol, um filamento de tungstênio a 2500 K, um metal aquecido a 1500 K, pele humana a 305 K e uma superfície metálica resfriada criogenicamente a 60 K. Estime a fração da emissão solar que se encontra nas seguintes regiões espectrais: ultravioleta, visível e infravermelha.

Passo 1

Vamos começar estimando os comprimentos de onda máximos para cada uma das superfícies pedidas, ok?

Só precisamos resolver a equação 12.31 para cada um:

λ m a x = C 3 T

E com C 3 = 2898   μ m   .   K vamos ter:

λ m a x ,   s o l = 2898 5800 λ m a x ,   t u n g s t ê n i o = 2898 2500 λ m a x ,   m e t a l   a q u e c i d o = 2898 1500

λ m a x ,   s o l = 0,50   μ m λ m a x ,   t u n g s t ê n i o = 1,16   μ m λ m a x ,   m e t a l   a q u e c i d o = 1,93   μ m

Mas ainda faltam dois, vamos continuar:

λ m a x ,   p e l e   h u m a n a = 2898 305 λ m a x ,   m e t a l   r e s f r i a d o = 2898 60

λ m a x ,   p e l e   h u m a n a = 9,50   μ m λ m a x ,   m e t a l   r e s f r i a d o = 48,3   μ m

Passo 2

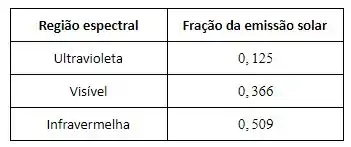
Agora na segunda parte, o enunciado quer a fração da emissão solar nas regiões espectrais ultravioleta, visível e infravermelha…

Vamos começar visitando a figura 12.3 e vendo os limites do comprimento de onda de cada região espectral:

Ultravioleta: 0,01   μ m   -   0,4   μ m

Visível: 0,4   μ m   -   0,7   μ m

Infravermelha: 0,7   μ m   -   100   μ m

Agora que temos os comprimentos de onda, e como estamos buscando a fração da emissão solar vamos usar a temperatura do sol de T = 5800   K , teremos o seguinte:

λ   .   T u l t r a v i o l e t a = 0,4   .   5800 = 2320

λ   .   T v i s í v e l = 0,7   .   5800 = 4060

λ   .   T i n f r a v e r m e l h a = 100   .   5800 = 580000

Agora vamos visitar a tabela 12.2 e encontrar o valor de F 0 → λ para cada valor de ( λ   .   T ) que encontramos aqui em cima:

F 0 → λ u l t r a v i o l e t a = 0,125

F 0 → λ v i s í v e l = 0,491

F 0 → λ i n f r a v e r m e l h a = 1

E agora finalmente vamos ter:

F u l t r a v i o l e t a = 0,125 - 0 = 0,125

F v i s í v e l = 0,491 - 0,125 = 0,366

F i n f r a v e r m e l h a = 1 - 0,491 = 0,509

Show! Conseguimos!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma pequena superfície negra de área A = 3,5 cm² mantida a 750 K. Determine a taxa em que a energia de radiação é emitida pela superfície através da abertura em forma de anel, definida por 0
Um sensor de radiação e uma pequena superfície de área A1, ambos emitentes de radiação do corpo negro, são orientados como mostra a figura abaixo. Determine a distância L onde o sensor mede 2/3 da tax
Um recipiente tem uma área superficial interna de 100 m2 , e esta superfície, que é mantida a uma temperatura constante, é preta. Uma pequena abertura no recipiente tem uma área de 0,02 m2 . A taxa de
Propõe-se que as temperaturas extremamente altas necessárias para disparar a fusão nuclear sejam geradas pela irradiação com laser de uma pequena partícula de deotério e trítio com diâmetro Dp = 1,8 m
Um método proposto para geração de eletricidade a partir da irradiação solar é concentrar a irradiação no interior de uma cavidade que é colocada no interior de um grande recipiente de um sal com alto