Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 130
Dois reservatórios são conectados por meio de três tubos limpos de ferro fundido em série, L1 = 600 m, D1 = 0,3 m, L2 = 900 m, D2 = 0,4 m, L3 = 1500 m e D3 = 0,45 m. Para uma vazão de 0,11 m3/s de água a 15ºC, determine a diferença de elevação entre os reservatórios.
Passo 1
Oi pessoal, tudo bem ?
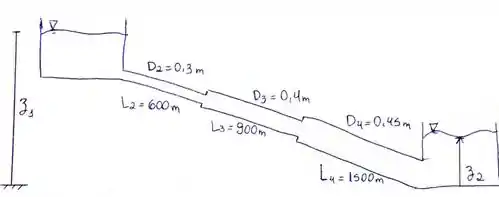
Essa é a representação do nosso problema
Como sabemos, para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da energia:
Considerações: Como a água consiste em um reservatório, consideramos que
Ao considerar os tanques elevados, estima-se que
é representa a velocidade do reservatório 2.
As perdas de carga são dadas pela eq da perda de carga maior, somada com as de perda de carga menor tanto no início da tubulação quanto no final, resultando em:
Passo 2
Analisemos primeiramente a seção 2:
O Número de Reynolds é dado por:
Lembrando que são retirados de acordo com as condições de temperatura da água do Apêndice A, neste caso, a .
Retiramos também o valor da rugosidade da Tabela 8.1, devido o material dos dutos.
Como o escoamento é turbulento, encontra-se o fator de atrito por:
)
Utilizando a ferramenta Solve do excel, foi possível determinar o fator de atrito
Passo 3
Analisemos a seção 3:
O Número de Reynolds é dado por:
Utilizando a ferramenta Solve do excel, foi possível determinar o fator de atrito
Passo 4
Analisemos agora a seção 4:
O Número de Reynolds é dado por:
Utilizando a ferramenta Solve do excel, foi possível determinar o fator de atrito
Passo 5
Então, é possível determinar a soma das perdas de carga dos dutos:
Ao substituir os valores na equação, têm-se que:
Da tabela 8.2, sabemos que
Portanto, reescrevendo a equação da perda de carga com as considerações feitas:
Resposta
Portanto, a diferença de nível entre os reservatórios é: