Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 24
Dois tanques com água a 20°C são conectados por um tubo capilar de 4 mm de diâmetro e 3,5 m de comprimento. A superfície do tanque 1 está 30 cm acima da superfície do tanque 2. (a) Estime a vazão em m³/h. O escoamento é laminar? (b) Para que diâmetro de tubo será igual a 500?
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!
Para água temos que e
Vamos olhar para nosso problema físico?
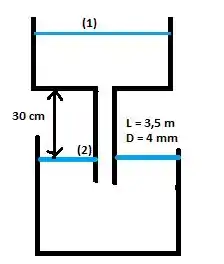
Aplicando nossa equação da energia, teremos que:
Bem, se você olhar no nosso desenho, temos que o ponto 1 e 2 tem suas pressões iguais a atmosférica. Além disso, como é de costume, as velocidades em superfícies de tanques podem ser aproximadas para zero, ou seja, nossa equação se reduzirá em:
Passo 2
(a) Vamos assumir que nosso escoamento é laminar, beleza? Isso vai fazer com que a gente consiga escrever nossa perda de carga hf da seguinte maneira:
Mas não podemos simplesmente achar que já encontramos a vazão! A gente precisou assumir que o escoamento era laminar, então temos que comprovar isso.
Show, então nossa hipótese estava correta e realmente a vazão é de 0,02 m³/h
Passo 3
(b) Se
A gente aqui tem duas variáveis né? O valor do diâmetro e o valor da vazão, porque não sabemos qual é o valor de vazão que nos deu .
Então precisamos de mais uma equação independente para o fechamento de equações. E qual será essa equação?
Resolvendo essas duas equações teremos que:
Resolvendo essas duas equações a gente obtém que e que o diâmetro será de 2,67 mm