Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 14

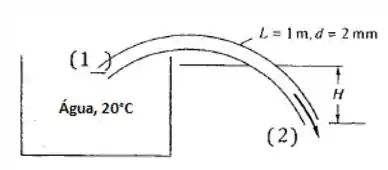
Água a 20°C deve ser retirada por sifão por um tubo de 1 m de comprimento e 2 mm de diâmetro, como na figura a seguir. Existe alguma altura H para a qual o escoamento não é laminar? Qual é a vazão se H = 50 cm? Despreza a curvatura do tubo.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Primeiro vamos logo pegar as propriedades da água em 20°C, show?

ρ = 998 k g m 3

μ = 0,001   k g / ( m . s )

Vamos escrever nossa equação de energia entre o ponto (1) e ponto (2)!!

p a t m ρ g + V 1 2 2 g + z 1 = p a t m ρ g + V 2 2 2 g + z 2 + h f

Note que no ponto 1, estaríamos na superfície da água dentro do tanque, e nesses casos temos que as velocidades são aproximadas para 0 nas superfícies de um tanque.

z 1 - z 2 = V 2 2 2 g + h f

H - V 2 2 2 g = h f

Mas quem é a nossa perda de carga hf?? Bem, temos que considerar o escoamento laminar (afinal, o próprio enunciado nos questiona se há alguma altura H pra ele não ser laminar)

H - V 2 2 2 g = h f = 32 μ L ρ g d 2 V

Passo 2

Agora qual é o paranauê que vamos fazer?

Bora substituir nossos valores dentro da nossa equação final do passo 1 e obter o valor de V!!!

0,5 - V 2 2 9,81 = 32 0,001 1 V 998 9,81 0,002 2 → V = 0,6   m / s

Note que temos uma equação quadrática, né? Então vamos ter duas raízes!!! Eu já deixei pra você qual é a raiz positiva!!

Passo 3

Uma vez que conhecemos a velocidade, agora podemos calcular nossa bendita e linda vazão volumétrica!

Q = A V = π 4 d 2 V = π 4 0,002 2 0,6 = 1,85 m 3 s   x 3600 s h = 0,0067 m 3 h

Note que essa conta foi feita utilizando a equação do passo (2) considerando que a altura H era igual a 50 cm, beleza? Importante deixar isso bem claro!!!

Bem, vamos testar então o valor de Re, afinal, se na altura H = 50 cm, o escoamento for laminar, certamente para qualquer valor abaixo dele, ainda teremos escoamento laminar também!

R e = ρ V D / μ = 998 0,6 0,002 0,001 = 1180   ( L a m i n a r )

Passo 4

É possível aproximarmos esse valor de Re para 2000 (que tá ali no limbo dos livros que diz sobre o valor de transição de regime laminar para turbulento) para H

Se você for testando os valores crescentes de H até 1 m, vai observar que o valor máximo de H que mantém o escoamento ainda com Re em torno de 2000 é até um H = 0,87 m

Resposta

  1. Q = 0,0067   m 3 / h
  2. Laminar até uma altura de H = 0,87 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa através de um tubo de 50 mm de diâmetro que subitamente contrai-se para 25 mm. A queda de pressão através da contração é 3,45 kPa. Determine a vazão volumétrica.
Água escoa a 25 L/s através de uma constrição suave, em que o diâmetro do tubo é reduzido de 75 mm para 37,5 mm, segundo um ângulo de 150°. Se a pressão antes da constrição for 500 kPa, estime a press
Ar escoa para fora de uma câmara de teste de uma sala limpa através de um duto de 150 mm de diâmetro e de comprimento L. O duto original tinha uma entrada de borda-viva, mas essa foi substituída por o
Um difusor cônico, com 150 mm de comprimento, é usado para expandir um tubo de um diâmetro de 50 mm para um diâmetro de 89 mm. Para uma vazão de água de 47 L/s, estime o aumento na pressão estática. Q
Encontrou-se espaço para a instalação de um difusor cônico, com comprimento de 0,45 m, no sistema de ventilação da sala limpa descrito no Problema 8.106. O melhor difusor com este comprimento deve ser