Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 74
Dois tubos com comprimento e materiais idênticos estão conectados em paralelo. O diâmetro do tubo A é o dobro do diâmetro do tubo B. Considerando o fator de atrito igual em ambos os casos e desprezando as perdas menores, determine a vazão nos dois tubos.
Passo 1
Oi pessoal, tudo bem?
Primeiramente, para o problema, assumimos que:
1. O fluxo é constante e incompressível.
2. O fator de atrito é o mesmo para os dois tubos.
3. Pequenas perdas são insignificantes.
O esboço do problema descrito pode ser expresso como:
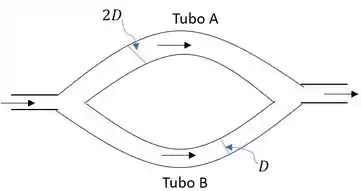
Passo 2
Vamos lá!
Quando dois tubos são paralelos em um sistema de tubulação, a perda de carga para cada tubo deve ser a mesma.
Como as perdas menores são desconsideradas, a perda de carga para fluxo totalmente desenvolvido em um tubo de comprimento L e diâmetro D pode ser expressa como:
Assim, podemos isolar a vazão:
Onde k é uma constante de proporcionalidade.
Passo 3
Quando o comprimento do tubo, o fator de atrito e a perda de carga são constantes, como é o caso da conexão paralela, o fluxo a taxa se torna proporcional à (2.5) potência do diâmetro.
Portanto, quando o diâmetro é dobrado, a vazão será aumento de . Podemos mostrar, através dos cálculos. Seja a vazão em A:
A vazão em B, portanto é:
Resposta
Portanto, a taxa de vazão nos dois tubos é de 5,66.