Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas Abrangentes - Ex. 3

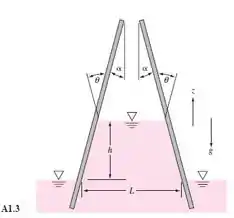
Duas placas finas, inclinadas de um ângulo α , são colocadas em um tanque contendo líquido com uma tensão superficial conhecida Υ e ângulo de contato θ , como mostra a Figura A1.3. Na superfície libre do líquido no tanque, as duas placas estão separadas por uma distância L e tem largura b para dentro da página. O líquido sobe uma distância h entre as placas, como mostra a figura.

  1. Qual é a força ascendente total (na direção z), devida à tensão superficial, agindo na coluna de líquido entre as placas?
  2. Se a massa específica do líquido for ρ , encontre uma expressão para a tensão superficial Υ em função das outras variáveis.

Passo 1

Bora lá pra mais uma!

Vou colocar um esqueminha pra gente manjar como faz a (a), olha só:

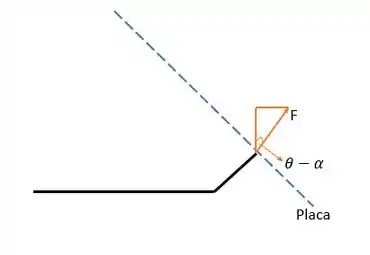
Nota que eu peguei o lado direito ali. Agora vamo lá, a tensão superficial segue tangente a superfície líquida no ponto de contato entre o líquido e a placa, daí, ela é essa força F. Essa força F tem magnitude dada por F = Υ b .

Queremos saber a componente vertical dessa força nas duas placas, assim, pelo triângulo retângulo, teremos que:

F z = 2 F cos ⁡ ( θ - α ) = 2 Υ b cos ⁡ ( θ - α )

Passo 2

Vamos para a (b). A força em z que achamos em (a) sustenta todo peso da coluna de líquido entre as placas, esse peso é obtido através do peso específico, da gravidade e de uma relação trigonométrica em um perfil da placa, assim:

P = ρ g b h ( L - h tan ⁡ α )

Igualando o peso e a força em z, teremos que:

Υ = ρ g b h L - h tan ⁡ α 2 cos ⁡ θ - α

Resposta

  1. F z = 2 Υ b cos ⁡ ( θ - α )
  2. Υ = ρ g b h L - h tan ⁡ α 2 cos ⁡ θ - α
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma certa corda pode suportar uma tensão máxima de 40N sem se partir. Uma criança amarra uma pedra de 0,37k g em uma das extremidades da corda e, segurando a outra extremidade, faz a pedra girar em um
Refaça os dois diagramas de movimento mostrados na figura P 5.29 , depois desenhe um vetor ao lado de cada um deles mostrando a orientação da força resultante exercida sobre o objeto. Explique seu rac
Uma única força, com componente F x , é exercida sobre um objeto de 500 g enquanto ele se move em longo do eixo x . Um gráfico da força F xv e r s u st é mostrado na figura P 5.32 . Desenhe um gráfico
Refaça os dois diagramas de movimento mostrados na figura P 5.28 , depois desenhe um vetor do lado de cada um deles mostrando a orientação da força resultante exercida sobre o objeto. Explique seu rac
Uma única força, com componente F x , é exercida sobre um objeto de 2 k g enquanto ele se move em longo do eixo x . Um gráfico da força F xv e r s u st é mostrado na figura P 5.32 . Desenhe um gráfico