Exercícios de Escoamento sobre um Cilindro - Lista de Exercícios Resolvida

(Adaptada) Um tubo circular, com diâmetro externo de , é colocado em uma corrente de ar a e de pressão. O ar está em escoamento cruzado em relação ao tubo com uma velocidade de , enquanto a superfície externa do tubo é mantida a .

Qual é a taxa de transferência de calor saindo do tubo por unidade de comprimento?

(Adaptado) Um anemômetro de fio quente feito de platina é operado no modo de temperatura constante para medir a velocidade de um escoamento de hélio. O diâmetro do fio é de 20 micrometros, seu comprimento é de e a temperatura de operação é .

Calcule a taxa de calor considerando uma corrente de hélio a e .

(Adaptada) Uma linha de alta tensão, com de diâmetro, possui uma resistência elétrica e está transmitindo uma corrente de .

Se ar ambiente a e , encontra-se em escoamento cruzado sobrea a linha, qual é a temperatura da sua superfície?

Um fio metálico fino com diâmetro está posicionado transversalmente a uma passagem para determinar a velocidade do escoamento a partir de características da transferência de calor.

Uma corrente elétrica é passada através do fio para aquecê-lo e o calor é dissipado por convecção para o fluido em escoamento. A resistência elétrica do fio é determinada por medidas elétricas e sua temperatura é conhecida a partir desta resistência.

Para um fluido com número de Prandtl arbitrário, desenvolva uma expressão para a sua velocidade em termos da diferença entre a temperatura do fio e a temperatura da corrente livre do fluido.

Qual é a velocidade de uma corrente de ar a e , se um fio com de diâmetro atinge uma temperatura de enquanto dissipa ?

Para melhorar a dissipação térmica em um chip de silício, quadrado com , um pino de cobre é fundido à superfície do chip. O comprimento e o diâmetro do pino são e , respectivamente, e ar atmosférico a e está em escoamento cruzado em relação ao pino.

A superfície do chip, e portanto a base do pino, é mantida a uma temperatura de .

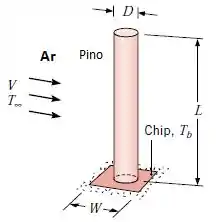
Supondo que o chip cause um efeito desprezível sobre o escoamento ao redor do pino, qual é o coeficiente convectivo médio na superfície do pino?

Desprezando a radiação e supondo que o coeficiente convectivo na extremidade do pino seja igual ao calculado na parta , determine a taxa de transferência de calor no pino.

Desprezando a radiação e supondo que o coeficiente de transferência de calor na superfície exposta do chip seja igual ao calculado na parte , determine a taxa total de transferência de calor saindo do chip.

Componentes eletrônicos cilíndricos com de diâmetro e de comprimento e que geram calor a uma taxa de , montados sobre uma placa de circuito impresso, são resfriados com ar escoando sobre eles com uma velocidade de .

Se a temperatura do ar é de , determine a temperatura da superfície dos componentes.

Suponha que você tenha uma escolha entre duas aletas pino. Uma possui uma área de seção reta quadrada com de lado e de altura e outra possui uma área de seção reta circular com de diâmetro e de altura.

Ambas são construídas de alumínio puro (propriedades à ). Em torno de cada aleta existe um ar circulando em velocidade de e temperatura de temperatura do meio é .

Assuma que o ar possui propriedades constantes e iguais a seu valor a 300 K. A base da aleta está a . Qual dessas terá a melhor relação (mais favorável em termos térmicos) de taxa de transferência de calor por peso de material para compor a aleta?

Despreze eventuais efeitos de convecção natural.

Considere um tanque de água quente de de diâmetro e de comprimento. O reservatório é colocado sobre o telhado de uma casa. A água dentro do tanque é aquecida a por um coletor solar de uma placa plana durante o dia.

O reservatório é então exposto ao ar a com vento a uma velocidade média de durante a noite.

Estime a temperatura do reservatório durante um período de . Assuma que a superfície do tanque esteja na mesma temperatura que a água no interior e o coeficiente de transferência de calor nas superfícies superior e inferior seja o mesmo das superfícies laterais.