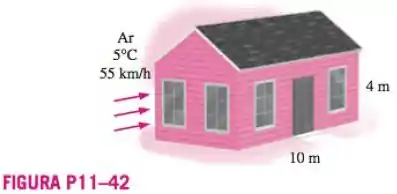
Durante um dia de inverno, sopra um vento a , e paralelo à parede de uma casa com de altura e de comprimento. Supondo que as superfícies das paredes sejam lisas, determine o arrasto de atrito que age sobre a parede. Qual seria a sua resposta se a velocidade do vento fosse o dobro? Quão realístico é tratar o escoamento sobre superfícies de parede laterais como escoamento sobre placa plana?

Vamos também separar os dados fornecidos no problema.

Velocidade do vento:

Velocidade do vento dobrada:

Temperatura do ar:

Pressão do ar:

Altura da parede:

Comprimento da parede:

Área da parede:

Vamos precisar também encontrar algumas propriedade na Tabela A-9 a e .

Densidade do ar:

Viscosidade cinemática do ar:

Agora, vamos calcular o número de Reynolds no final da parede, ou seja, a da parede para a velocidade de , usando a seguinte relação:

Aqui,  é a velocidade do escoamento,  é o comprimento da parede e  é a viscosidade cinemática do fluido. Substituindo os termos da relação acima pelos dados coletados, temos:

Nós supomos que o valor do número de Reynolds crítico é . Como o valor obtido do número de Reynolds é maior que o valor crítico, o escoamento é misto. Então, podemos calcular o coeficiente de atrito usando a expressão abaixo:

Substituindo o número de Reynolds encontrado no passo anterior, temos:

Aqui, como o arrasto de pressão é zero, e, portanto, para uma placa plana, a força de arrasto que atua na superfície da parede pode ser calculada usando a fórmula abaixo:

Onde,  é a densidade do ar,  é a área da parede através da qual o ar está fluindo e  é a velocidade do fluxo. Substituindo os termos da equação acima pelos dados coletados e calculados, temos:

Portanto, a força de arrasto que atua na parede quando a velocidade é é .

Tudo tranquilo até aqui?? Bora continuar então!!

Temos o caso em que a velocidade do escoamento é dobrada, assim, a nova velocidade é . Vamos refazer então todos os cálculos feitos acima mudando a velocidade. Temos que o número de Reynolds é o seguinte:

Aqui,  é a velocidade do escoamento,  é o comprimento da parede e  é a viscosidade cinemática do fluido. Substituindo os termos da relação acima pelos dados coletados, temos:

Nós supomos que o valor do número de Reynolds crítico é . Como o valor obtido do número de Reynolds é maior que o valor crítico, o escoamento é misto. Então, podemos calcular o coeficiente de atrito usando a expressão abaixo:

Substituindo o número de Reynolds encontrado no passo anterior, temos:

Aqui, como o arrasto de pressão é zero, e, portanto, para uma placa plana, a força de arrasto que atua na superfície da parede pode ser calculada usando a fórmula abaixo:

Onde,  é a densidade do ar,  é a área da parede através da qual o ar está fluindo e  é a velocidade do fluxo. Substituindo os termos da equação acima pelos dados coletados e calculados, temos:

Portanto, a força de arrasto que atua na parede quando a velocidade é é . A força de arrasto quase quadruplica quando a velocidade é dobrada. Isso é esperado, já que a força de arrasto é proporcional ao quadrado da velocidade e o efeito da velocidade no coeficiente de atrito é pequeno.

Tratar o escoamento sobre a parede lateral de uma casa como o escoamento sobre uma placa plana não é muito realista. Quando o fluxo atinge um corpo como uma casa, ele se separa no canto agudo e uma bolha de separação existe na maioria dos painéis laterais da casa. Portanto, as equações da camada limite da placa plana não são apropriadas para esse problema, e toda a casa deve ser considerada na solução.

Observe que o arrasto real provavelmente será muito maior, pois as superfícies da parede são tipicamente muito ásperas. Além disso, podemos resolver esse problema usando a relação de escoamento turbulento (em vez da relação de fluxo laminar-turbulento combinada) sem muita perda de precisão.