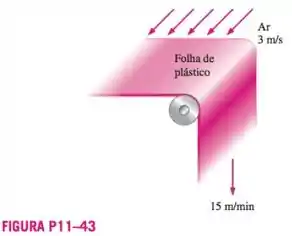
A seção de laminação de uma fábrica de plásticos produz uma folha contínua de plástico que tem de largura e de espessura a uma razão de . A folha de plástico está sujeita a um escoamento de ar a uma velocidade de em ambos os lados ao longo de suas superfícies normal à direção do movimento da folha. A largura da seção de refrigeração do ar é tal que um ponto fixo na folha de plástico passa através daquela seção em . Usando propriedades do ar a e , determine a força de arrasto que o ar exerce sobre a folha de plástico na direção do escoamento do ar.

Vamos também separar os dados fornecidos no problema.

Largura da folha de plástico:

Espessura da folha de plástico:

Tempo que a folha passa pelo resfriamento:

Velocidade da folha:  

Velocidade do fluxo de ar:  

Pressão do ar:

Temperatura do ar:

Vamos precisar também encontrar algumas propriedade na Tabela A-9 a e .

Densidade do ar:

Viscosidade cinemática do ar:

Agora, vamos calcular o número de Reynolds para o processo de resfriamento, usando a seguinte relação:

Aqui,  é a velocidade do escoamento,  é o comprimento folha de plástico sendo resfriado através da qual o ar está fluindo e  é a viscosidade cinemática do fluido. O ar está fluindo através da largura , portanto, o comprimento característico .

Substituindo os dados coletados na equação do numero de Reynolds, temos o seguinte:

Nós supomos que o valor do número de Reynolds crítico é . Como o valor obtido do número de Reynolds é menor, o escoamento é laminar. Então, podemos calcular o coeficiente de atrito usando a expressão abaixo:

Substituindo o número de Reynolds encontrado no passo anterior, temos:

Aqui o ar flui através de um ponto específico da placa por 2 segundos porque a placa está se movendo; portanto, aqui o comprimento da placa  é o comprimento pelo qual o ar flui por 2 segundos, que pode ser encontrado da seguinte maneira:

Logo, a área em ambos os lados da folha exposta ao fluxo de ar é:

Agora, podemos calcular a força de arrasto que atua nas superfícies superior e inferior da folha de plástico usando a fórmula abaixo:

Onde,  é a densidade do ar,  é a área da folha de plástico através da qual o ar está fluindo e  é a velocidade do fluxo. Substituindo os termos da equação acima pelos dados coletados e calculados, temos:

Portanto, a força de arrasto que atua na folha de plástico quando a velocidade do ar é é .