Durante um experimento com alto número de Reynolds, a força de arrasto total agindo sobre um corpo esférico de diâmetro D = 12c m submetido a um escoamento de ar a 1a t m e 5 ° C é medida como 5,2N . O arrasto de pressão agindo sobre o corpo é calculado integrando-se a distribuição de pressão (medida usando-se sensores de pressão através da superfície) resultando em 4,9N . Determine o coeficiente de arrasto de atrito da esfera.

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 24

Durante um experimento com alto número de Reynolds, a força de arrasto total agindo sobre um corpo esférico de diâmetro submetido a um escoamento de ar a e é medida como . O arrasto de pressão agindo sobre o corpo é calculado integrando-se a distribuição de pressão (medida usando-se sensores de pressão através da superfície) resultando em . Determine o coeficiente de arrasto de atrito da esfera.

Passo 1

Vamos começar esquematizando a nossa situação:

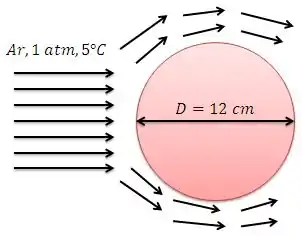
Temos ar a escoando sobre uma esfera de diâmetro . A força de arrasto total foi de , enquanto que a força de pressão foi .

Considerando que o escoamento possuía um alto número de Reynolds, devemos obter o coeficiente de arrasto de atrito. Vamos lá?

Passo 2

Como nosso primeiro passo, vamos calcular a força de arrasto do atrito. Para isso, vamos relembrar que:

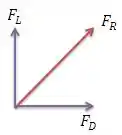
As forças de sustentação e atrito são perpendiculares e, que a resultante é a soma vetorial delas.

Usando o bom e velho teorema de Pitágoras:

Tudo bem até aqui?

Nosso próximo passo será encontrar a velocidade de escoamento.

Passo 3

Recebemos a informação de que o experimento ocorre em um alto número de Reynolds. Para escoamento sobre uma esfera, podemos assumir que é um valor alto. O número de Reynolds é dado por:

Então, para encontrarmos a velocidade de escoamento, vamos primeiro encontrar as propriedades do ar a . Pela tabela do apêndice do livro:

Aplicando este valor:

Passo 4

Por fim, podemos obter o coeficiente de atrito de arrasto a partir da relação:

Para uma esfera, a área projetada é:

Aplicando na relação do coeficiente de arrasto:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em voo de planeio (sem potência), a sustentação e o arrasto estão em equilíbrio com o peso. Mostre que, se não houver vento, a aeronave desce com um ângulo tan ⁡ θ ≈ a r r a s t o s u s t e n t a ç ã

80 – A bela expressão para a sustentação de um aerofólio bidimensional, eq. 8.72, surge da aplicação da transformação de Joukowski, ζ = z + a 2 z Em que, z = x + i y ;ζ = η + i β A constante a é uma e

Suppose that the airplane of Prob. P7.116 is fi tted with allthe best high-lift devices of Fig. 7.28. What is its minimumstall speed in mi/h? Estimate the stopping distance if theplane lands at V0 5 1

The so-called Rocket Man, Yves Rossy, fl ew across the Alps in2008, wearing a rocket-propelled wing-suit with the followingdata: thrust 5 200 lbf, altitude 5 8,200 ft, and wingspan 5 8 ft(http://en.wi

The Transition® auto-car in Fig. 7.30 has a weight of 1200lbf, a wingspan of 27.5 ft, and a wing area of 150 ft2, with a symmetrical airfoil, CDq Toyota Prius [21], CDA provides a thrust of 250 lbf, h