Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 12

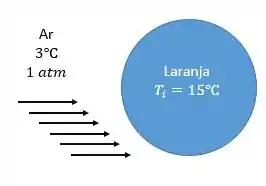
Durante o resfriamento a ar de laranjas, uvas e tangerinas, o coeficiente combinado de transferência de calor por convecção, radiação e evaporação para velocidades do ar de 0,11 < V < 0,33   m / s é determinado experimentalmente e expresso como h = 5,05 k a r R e 1 3 D , onde o diâmetro D é o comprimento característico. As laranjas são resfriadas com ar refrigerado a 3 ℃ e 1   a t m a velocidade de 0,3   m / s . Determine (a) a taxa inicial de transferência de calor a partir de uma laranja de 7   c m de diâmetro inicialmente a 15 ℃ , com condutividade térmica de 0,70   W m   K ,) (b) o valor inicial do gradiente de temperatura na superfície interna da laranja e (c) o valor do número de Nusselt.

Passo 1

A questão fornece a relação para determinação do coeficiente convectivo de troca térmica para algumas frutas, e considerando as condições de operação estáveis, a laranja como um corpo esférico, o coeficiente convectivo de troca térmica constante em toda a superfície e as propriedades da água sendo utilizadas para a laranja, devemos determinar a taxa inicial de transferência de calor, o gradiente de temperatura na superfície e o número de Nusselt.

Tem-se que a condutividade térmica da laranja é dada e a do ar se calcula da seguinte maneira:

T f =   T s +   T ∞ 2 =   15 + 5 2 = 10 ℃

Visitando a tabela A-15, ficamos então com:

k = 0,02439   W / m ℃

E desse mesmo jeito, encontramos a viscosidade cinemática, sendo ela:

v = 1,426 × 10 - 5 m 2 / s .

Passo 2

Agora resolvendo a letra a, precisamos calcular a taxa inicial de transferência de calor, e para isso temos que calcular algumas coisinhas…

Primeiro a área superficial da laranja:

A s =   π D 2

A s =   π 0,07 m 2

A s = 0,01539   m ²

Agora precisamos do número de Reynolds do sistema:

R e = V D v

R e =   0,3 m s 0,07 m 1,426 × 10 - 5 m 2 s

R e = 1473

E ainda precisamos do coeficiente:

h =   5,05 k a r R e 1 3 D

h =   5,05 ( 0,02439 W m ℃ ) ( 1473 ) 1 / 3 0,07 m

h = 20,02 W m ² K

Agora sim! A transferência de calor será:

Q ˙ = h A s T s -   T ∞

Q ˙ = 20,02 W m 2 K 0,01539   m 2 15 ℃ - 3 ℃

Q ˙ = 3,70   W

Passo 3

Agora para a letra b, temos que encontrar o gradiente de temperatura na superfície da laranja… Ele pode ser obtido da seguinte maneira:

q ˙ c o n v =   q ˙ c o n d =   - k ∂ T ∂ r | r = R = h ( T s -   T ∞ )

Opa! Então podemos fazer:

∂ T ∂ r | r = R =   - h T s -   T ∞ k

Substituindo os dados do enunciado, temos:

∂ T ∂ r | r = R =   - 20,02 W m 2 K 15 ℃ - 3 ℃ 0,70 W m ℃

∂ T ∂ r | r = R =   - 343 ℃ / m

Passo 4

E pra fechar vamos de letra c! Temos que encontrar o número de Nusselt! Ele pode ser obtido pela seguinte relação:

N u =   h D k

N u =   20,02 W m 2 K 0,07 m 0,02439 W m ℃

N u = 57,5

Prontinho!

Resposta

a   Q ˙ = 3,70 W

b ∂ T ∂ r | r = R =   - 343 ℃ m

c N u = 57,5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Gás hélio a uma temperatura de corrente livre de T ∞ = 25°C está em fluxo paralelo sobre uma placa plana de comprimento L = 3m e temperatura T s = 85°C . Entretanto, os obstáculos colocados no fluxo i
Ar atmosférico escoa paralelamente ( u ∞ = 1 0m / s ,T ∞ = 15 ° C ) sobre a superfície plana de um aquecedor que deve ser mantida a uma temperatura de 9 0 ° C . A área da superfície do aquecedor é de
Escoamento laminar normalmente persiste em uma placa plana e lisa até um certo valor cítico do número de Reynolds seja alcançado. No entanto,o fluxo pode ser alterado para um estado de regime turbulen
Considere as condições do exemplo 6.4. A camada-limite pode ser levada a um estado de regime turbulento em x = x r pela aplicação de rugosidades na superfícies da placa plana em x r . Calcule os valor
Qual é a diferença entre convecção mássica e contribuição convectiva?