Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 7
Durante o resfriamento de batatas ao ar, o coeficiente combinado de transferência de calor por convecção, radiação e evaporação é determinado experimentalmente, desta forma:
Considere uma batata de de diâmetro, inicialmente a , com condutividade térmica de . As batatas são refrigeradas com ar refrigerado a , na velocidade de . Determine a taxa inicial de transferência de calor a partir da batata e o valor inicial do gradiente de temperatura em sua superfície.
Passo 1
Primeiramente, é interessante fazer um desenho que represente a situação descrita no problema. O esquema é esse aqui:
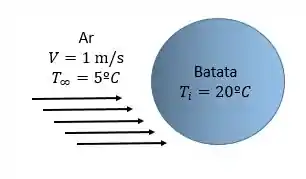
E para iniciar a resolução, pode-se assumir que a batata é esférica, já que temos o diâmetro, as condições operacionais são estáveis e o coeficiente convectivo de troca térmica é constante em toda a superfície da batata. Além disso, a questão também fornece a condutividade térmica .
Passo 2
De posse dos dados do problema, pode-se calcular a área superficial da batata, para a obtenção da taxa inicial de transferência de calor da batatas:
Observando que o valor de é obtido observando a tabela, no valor correspondente à velocidade em questão.
Passo 3
O valor inicial do gradiente de temperatura na superfície da batata pode ser calculado da seguinte maneira: