Durante o tratamento térmico por radiação de um material na forma de uma fina película, sua forma, que pode ser hemisférica (a) ou esférica (b), é mantida por uma pressão de ar relativamente baixa (como no caso de um balão de borracha). A irradiação sobre a película é devido à emissão de um aquecedor radiante com área , que emite de forma difusa com uma intensidade Durante o tratamento térmico por radiação de um material na forma de uma fina película, sua forma, que pode ser hemisférica (a) ou esférica (b), é mantida por uma pressão de ar relativamente baixa (como no caso de um balão de borracha). A irradiação sobre a película é devido à emissão de um aquecedor radiante com área , que emite de forma difusa com uma intensidade

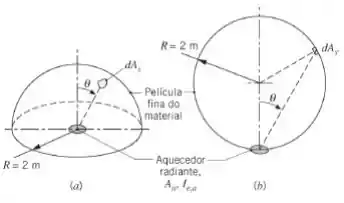
(a) Obtenha uma expressão para a irradiação sobre a película como uma função do ângulo de zênite .

(b) Com base nas expressões obtidas na parte (a), qual forma proporciona a irradiação mais uniforme e, portanto, possibilita um melhor controle de qualidade no processo de tratamento?

Para resolver essa questão vamos assumir que o aquecedor emite difusamente e que toda a radiação que sai do aquecedor é absorvida pela película fina. A irradiação em qualquer área diferencial, , devido à emissão do aquecedor , é:

Onde é a taxa de calor radiante deixando e interceptada por .

E é o ângulo sólido que subtende em relação a qualquer ponto em .

Onde é normal para a direção de visualização e é a distância de separação.

Para o hemisfério o ângulo sólido é,

E a distribuição de irradiação na superfície hemisférica em função de é,

Para a esfera o ângulo sólido é,

Onde , a partir da geometria do cordão da esfera e raios com , é:

E a distribuição de irradiação na superfície esférica em função de é,

Para a forma esférica, a irradiação no filme fino é uniforme e, portanto, proporciona um melhor controle de qualidade para o processo de tratamento.

Substituindo os valores numéricos, as irradiações são: