Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 9

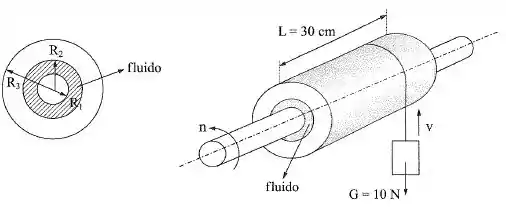
O eixo da figura, ao girar, provoca a rotação do tambor. Este enrola a corda, que levanta um peso de 10   N com uma velocidade constante de 0,5   m / s . O fluido existente entre o eixo e o tambor tem μ = 0,1   N ⋅ s / m 2 e apresenta um diagrama linear de velocidades. Pede-se:

  1. A rotação do eixo em rpm;
  2. O momento provocado pelo fluido contra a rotação do eixo.

Dados: R 1 = 10   c m ; R 2 = 10,1   c m ; R 3 = 20   c m ; ω = 2 π r .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para determinar a rotação do eixo, temos que relacionar os momentos do enunciado.

M t = M G

Desenvolvendo, temos que:

τ ⋅ A ⋅ R 2 = G ⋅ R 3

Substituindo τ = μ ∆ u y e A = 2 π R 2 L , temos que:

μ ∆ u y 2 π R 2 L R 2 = G R 3

Sabemos que:

y = R 2 - R 1

y = 10,1 - 10 = 0,1   c m

Passo 2

Isolando o termo da velocidade, teremos que:

∆ u = G R 3 y μ 2 π L R 2 2

Substituindo os valores, temos que:

∆ u = 10 × 0,2 × 0,1 × 10 - 2 0,1 × 2 π × 0,3 × 0,101 2

∆ u = 1,04   m / s

Passo 3

Podemos encontrar uma relação para as velocidades a partir dos raios. Temos que:

u 2 = u 3 R 2 R 3

Resolvendo, temos que:

u 2 = 0,5 0,101 0,2

Sabemos também que:

u 1 = ∆ u + u 2

Substituindo os valores, temos que:

u 1 = 1,04 + 0,2525

u 1 = 1,29   m / s

Passo 4

Com estes valores, podemos utilizar a seguinte fórmula para encontrar a rotação.

n 1 = u 1 2 π R 1

Substituindo os valores, temos que:

n 1 = 1,29 2 π R 1

n 1 = 1,29 2 π 0,1 × 60

Logo:

n 1 = 123   r p m

Passo 5

O momento no eixo, é dado por:

M e i x o = τ A 1 R 1

Desenvolvendo, temos que:

M e i x o = μ ∆ u y 2 π R 1 L R 1

M e i x o = 2 π μ ∆ u y L R 1 2

Substituindo os valores, temos que:

M e i x o = 2 π 0,1 1,04 0,1 × 10 - 2 0,3 0,1 2

O momento provocado pelo fluido contra a rotação do eixo é de:

M e i x o = 2   N ⋅ m

Resposta

a )   n 1 = 123   r p m

b ) M e i x o = 2   N ⋅ m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Enchalentamenteumcopodevidrocomáguaatéomáximonívelpossível.Observeoníveldaáguabemdeperto.Expliqueagora comoessenívelpodesersuperioraodabordadocopo.
Você pretende colocar cuidadosamente algumas agulhas de aço sobre a superfície livre da água em um grande tanque. As agulhas vêm em dois comprimentos: algumas com 5 cm e outras com 10 cm de compriment
A que velocidade mínima (em km/h) um automóvel teria que viajar para que os efeitos de compressibilidade fossem importantes? Considere que a temperatura local do ar atmosférico seja de 15,5°C.
Operfildevelocidadedacamada­limiteviscosa,mostradonaFig.2.15,podeseraproximadoporumaequaçãocúbica:Acondiçãolimiteéu=U(avelocidadedacorrentelivre)nabordalimiteθ(ondeoatritoviscososetornazero).Determine
A água é normalmente considerada como um fluido incompressível quando se avaliam variações na pressão estática. Na verdade, a água é 100 vezes mais compressível que o aço. Considerando que o módulo de