Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 84
O perfil de velocidade da camadalimite viscosa, mostrado na Fig. 2.15, pode ser aproximado por uma equação cúbica:
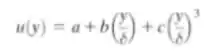
A condição limite é u = U (a velocidade da corrente livre) na borda limite θ (onde o atrito viscoso se torna zero). Determine os valores de a, b e c.
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Assumindo uma condição de não escorregamento, temos que no limite exterior:
Aplicando as condições:
Sabemos que:
Logo:
Das equações 1 e 2 (encontradas acima), temos que:
Portanto:
Resposta
Exercícios de Livros Relacionados
Um manômetro semelhante ao que foi descrito no Exercício 1.6ª continha mercúrio em vez de água. Admita que a pressão externa seja 760 Torr e que o lado aberto esteja 10 cm mais alto que o lado conecta
Um manômetro consiste de um tubo em forma de U que contém um liquido. Um lado esta ligado ao aparelho e outro esta aberto para a atmosfera.? A pressão no interior do aparelho é, então, determinada a p
Um eixo com 6,00c m de diâmetro está sendo empurrado axialmente para o interior de um mancal com 6,02c m de diâmetro e 40c m de comprimento. A folga, considerada uniforme, é preenchida com óleo cujas
Um cilindro sólido de diâmetro D , comprimento L e massa específica ρ s cai pelo efeito da gravidade no interior de um tubo de diâmetro D 0 . A folga, D 0 - D D , é preenchida com um fluido de massa e
O dispositivo na Figura P 1.56 é chamado de viscosímetro cone-placa. O ângulo do cone é muito pequeno, de forma que sen θθ , e a folga é preenchida com o líquido de teste. O torque M necessário para