Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 8

O dispositivo da figura é constituído de dois pistões de mesmas dimensões geométricas que se deslocam em dois cilindros de mesmas dimensões. Entre os pistões e os cilindros existe um lubrificante de viscosidade dinâmica 10 - 2   N ⋅ s / m 2 . O peso específico do pistão 1 é 20000   N ⋅ m 3 . Qual é o peso específico do pistão 2 para que o conjunto se desloque na direção indicada com uma velocidade de 2   m / s constante? Desprezar o atrito na corda e nas roldanas.

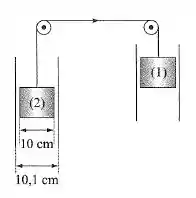
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para que exista equilíbrio, temos que a força viscosa em 1 é igual a força viscosa em 2 . Consideraremos ainda que a tração é igual ao peso do pistão mais a força tangencial provocada pelo lubrificante. Logo:

F μ 1 = F μ 2

F μ 1 = τ ⋅ A

F μ 1 = μ ⋅ u y ⋅ A

Substituindo os valores, temos que:

F μ 1 = 10 - 2 ⋅ 2 0,101 - 0,1 2 ⋅ A

F μ 1 = 40 A

Passo 2

Analisando a figura, temos a seguinte relação:

T = W 2 + 40 A

E:

W 1 = T + 40 A

Substituindo uma equação na outra encontramos:

W 1 = W 2 + 80 A

Passo 3

Sabendo que o peso específico é dado por:

γ = W V

Temos que:

γ 1 V = γ 2 V + 80 A

Dividindo os dois lados por V , temos que:

γ 1 = γ 2 + 80 A V

Temos que:

A V = 0,1 π L π 0,1 2 4 L

Resolvendo, temos que:

A V = 40

Substituindo os valores, temos que:

20000 = γ 2 + 80 ⋅ 40

Logo, o peso específico do pistão será:

γ 2 = 16800   N / m 3

Resposta

γ 2 = 16800   N / m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ocampodevelocidadeemque V → A x i ^ - A y j ^ , em que A = 2 s - 1 , pode ser interpretado para representar o escoamento em um canto.Determineumaequaçãoparaaslinhasde corrente do escoamento. Trace div
Umescoamentoédescritopelocampodevelocidade V → = A x + B i + - A y j , em que A = 3 m m m e b = 6 m s . Trace algumas linhas de corrente no plano x y , incluindo aquela que passa pelo ponto x , y = 0,
Paraoscamposdevelocidadedadosabaixo,determine: a.Seocampodeescoamentoéuni,bioutridimensional,eporquê. b.Seoescoamentoéemregimepermanenteoutransiente,eporquê.(Asquantidadesaebsãoconstantes.) 1 → V = a
Umlíquidoviscosoécisalhadoentredoisdiscosparalelos;odiscosuperiorgiraeoinferioréfixo.Ocampodevelocidadeentreos discosédadopor → V=ê θ ω z / h ê .(Aorigemdascoordenadasestálocalizadanocentrododiscoinfe
Umcampodevelocidadeédadopor V → = a x 3 i + b x y 3 j , em que a = 1 m - 2 s - 1 ,b = 1 m - 3 s - 1 . Determine a equação das linhas de corrente para qualquer tempo t . Trace diversas linhas de corren