Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 10

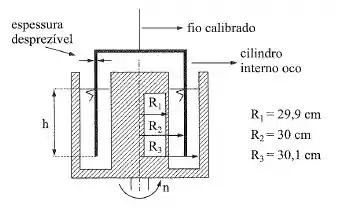
No viscosímetro da figura, o cilindro externo gira com uma rotação de 100   r p m constante. O cilindro interno é oco, sua parede tem espessura desprezível e está preso a um calibrado à torção. Esse cilindro gira torcendo o fio até que nele se atinja um momento de 10   N ⋅ m . Supondo o diagrama de velocidades linear e um líquido de viscosidade cinemática v = 10 - 4   m 2 / s e ρ = 2 = 800   k g / m 3 , qual é a altura do líquido?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para encontrarmos a altura, temos que encontrar o valor da velocidade do cilindro interno. Temos que:

u i = 2 π n R 1

Substituindo os valores e resolvendo, temos que:

u i = 2 π 100 60 0,299

u i = 3,13   m / s

Temos também que:

ε i = R 2 - R 1

ε i = 30 - 29,9 = 0,1   c m

Passo 2

Agora, vamos calcular a velocidade externa do cilindro.

V e = 2 π n R 3

Substituindo os valores, temos que:

u e = 2 π 100 60 0,301

u e = 3,15   m / s

E:

ε e = 30,1 - 30 = 0,1   c m

Passo 3

A viscosidade do fluido é dada por:

μ = v ⋅ ρ

μ = 10 - 4 800

μ = 0,08   N ⋅ s / m 2

Com esses valores, podemos aplicar na equação do momento, isolar a altura e encontrar a mesma.

M = μ u i ε i 2 π R 2 h R 2 + μ u e ε e 2 π R 2 h R 2

Passo 4

Vamos manipular a equação do momento do passo anterior:

M = μ u i ε i 2 π R 2 h R 2 + μ u e ε e 2 π R 2 h R 2

M = μ 2 π R 2 2 h ε u e + u i

Isolando h , temos que:

h = M ε μ 2 π R 2 2 u e + u i

Substituindo os valores, temos que:

h = 10 0,1 ⋅ 10 - 2 0,08 2 π 0,3 2 3,15 + 3,13

Portanto:

h = 0,035   m

Resposta

h = 0,035   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Paraoscamposdevelocidadedadosabaixo,determine: a.Seocampodeescoamentoéuni,bioutridimensional,eporquê. b.Seoescoamentoéemregimepermanenteoutransiente,eporquê.(Asquantidadesaeb sãoconstantes.) 1 v → = a
Ocampodevelocidadeédadopor V → = a x i - b t y j , em que a = 1 s - 1 ,b = 1 s - 2 . Determine a equação das linhas de corrente para qualquer tempo t . Trace diversas linhas de corrente no primeiro qu
A velocidade para um escoamento permanente incompressível no plano x y é dada por v → = i ^A / x+ j ^A / x 2 , em que A=2m 2 / s e as coordenadas são medidas em metros. Obtenha uma equação para a linh
Considere o campo de escoamento V → =a x ti ^+bj ^ , em que a=0,1s - 2 e b=4m / s . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y )=( 3 ,1 ) no instante t=0 , trac
Começando com o campo de velocidade do Problema 2.5, verifique que as equações paramétricas para o movimento da partícula são dadas por x p =c 1 e A t e y p = c 2 e - A t . Obtenha a equação para a tr