Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 3
Para o elemento triangular na Figura P1.3, mostre que a superfície livre inclinada de um líquido, em contato com uma atmosfera à pressão pa, deve estar sujeita à tensão de cisalhamento e por isso começa a escoar. Sugestão: considere o peso do fluido e mostre que uma condição de cisalhamento nulo causará forças horizontais desbalanceadas.
Passo 1
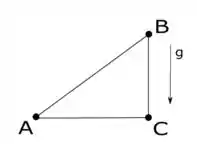
Beleza, podemos utilizar a sugestão dada no enunciado e supor que não há cisalhamento no sistema. Vamos primeiro colocar pontos no esquema para facilitar:
Passo 2
Podemos ver que as forças verticais sobre a reta AC crescem linearmente devido ao triângulo, sendo a maior força vertical sobre o ponto C, mas as forças verticais do fluido não produzem um desbalanceamento vertical.
Mas para as forças horizontais, o efeito da componente horizontal da gravidade do fluido aumenta conforme olhamos de B para A, porque haverá uma tensão de cisalhamento logo em B, e para cada ponto seguinte do fluido, haverá a componente do ponto mais o efeito de cada ponto anterior do fluído.
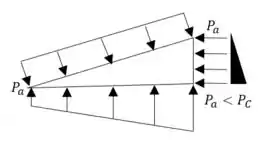
No diagrama de cargas abaixo podemos ver no triangulo na direita o aumento do efeito da tensão superficial do fluido conforme vamos do ponto B ao ponto A:
Resposta
Ei, a resposta está no passo a passo :)