Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 39

A emissividade direcional espectral de um material difuso a 2000 K apresenta a seguinte distribuição:

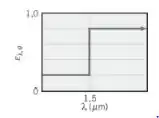
Determine a emissividade hemisférica total a 2000 K. Determine o poder emissivo na faixa espectral compreendida entre 0,8 e 2,5 μm e nas direções 0 ≤ θ ≤ 30°.

Passo 1

Precisamos primeiro encontrar o valor da emissividade, para isso vamos usar a equação:

ε T = ε 1   .   F 0 → 1,5   +   ε 2   .   1 -   F 0 → 1,5

E para encontrar o valor de F 0 → 1,5 , vamos fazer:

λ   .   T = 1,5   .   2000

λ   .   T = 3000   μ m   .   K

E visitando a tabela 12.2, temos que:

F 0 → 1,5 = 0,2732

Então vamos encontrar nossa emissividade:

ε 2000 = 0,2   .   0,2732   +   0,8   .   1 -   0,2732

ε 2000 = 0,636

Primeira parte prontinha!

Passo 2

Agora temos que achar o poder emissivo, vamos partir da equação 12.15:

Δ E = ∫ 0,8 2,5 ∫ 0 2 π ∫ 0 π / 6 ε λ ,   θ   .   I λ ,   b λ ,   T   .   c o s θ   .   s e n θ   .   d θ .   d φ   .   d λ

E se temos que:

I λ ,   e λ ,   θ ,   φ = ε λ ,   θ   .     I λ ,   b λ ,   T ε λ ,   θ = ε λ

Vamos ficar com:

Δ E = ∫ 0 2 π ∫ 0 π / 6   c o s θ   .   s e n θ   .   d θ .   d φ .   E b T π   .   ∫ 0,8 1,5 ε 1   .   E λ ,   b λ ,   T   .   d λ E b T   +   ∫ 1,5 2,5 ε 2   .   E λ ,   b λ ,   T   .   d λ E b T

Δ E = φ | 0 2 π   .   s e n ² θ 2 | 0 π / 6   .   σ   .   T 4 π   .   ε 1   .   F 0 → 1,5 - F 0 → 0,8 + ε 2   .   F 0 → 2,5 - F 0 → 1,5

E pra gente encontrar o F 0 → 0,8 e o F 0 → 2,5 , vamos encontrar primeiro:

λ   .   T = 0,8   .   2000 λ   .   T = 2,5   .   2000

λ   .   T = 1600   μ m   .   K λ   .   T = 5000   μ m   .   K

E indo lá na tabela 12.2, vamos ter que:

F 0 → 0,8 = 0,0197 F 0 → 2,5 = 0,6337

Pra finalizar agora vamos ter:

Δ E = 2 π   .   s e n ² π / 6 2 . 5,67   .   10 - 8   .   2000 4 π . 0,2 . 0,2732 - 0,0197 + 0,8 . 0,6337 - 0,2732

Δ E = 0,25   .   0,907   .   10 6   .   0,339

Δ E = 76885,2   W / m ²

ou

Δ E = 76,89   k W / m ²

Uhul! Conseguimos!!

Resposta

ε 2000 = 0,636 Δ E = 76,89   k W / m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a superfície direcionalmente seletiva que tem a emissividade direcional εθ mostrada a seguir.Supondo que a superfície seja isotrópica na direção ϕ, calcule a razão entre a emissividade norma
Uma superfície difusa é caracterizada pela distribuição de emissividades hemisféricas espectrais mostrada na figura. Considerando temperaturas superficiais na faixa de 300 ≤ Ts ≤ 1000 K, em qual tempe
A janela de uma grande câmara de vácuo é fabricada com um material com características espectrais conhecidas. Um feixe colimado de energia radiante, gerado por um simulador solar, incide sobre a janel
A vigia (com 50 mm de diâmetro) de uma grande fornalha operando a 450°C é coberta com um material que tem τ = 0,8 e ρ = 0 para a irradiação originada no interior da fornalha. O material tem uma emissi