Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 75
A janela de uma grande câmara de vácuo é fabricada com um material com características espectrais conhecidas. Um feixe colimado de energia radiante, gerado por um simulador solar, incide sobre a janela e tem um fluxo de 3000 W/m2 . As paredes internas da câmara, que são grandes quando comparadas à área da janela, são mantidas a 77 K. A superfície externa da janela está exposta a uma vizinhança e ao ar ambiente, ambos a 25°C, com um coeficiente de transferência de calor por convecção de 15 W/(m2 · K).
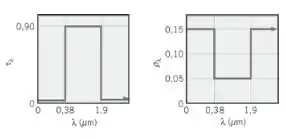
- Determine a transmissividade do material da janela em relação à radiação do simulador solar, que tem uma distribuição espectral aproximadamente igual à do Sol.
- Admitindo que a janela esteja isolada termicamente da sua estrutura de fixação à câmara, qual é a temperatura que ela atingirá em condições de regime estacionário?
- Calcule a transferência radiante líquida, por unidade de área da janela, para a parede da câmara de vácuo, excluindo o fluxo solar simulado que é transmitido.
Passo 1
Nosso enunciado quer que a gente resolva três letrinhas… Vamos começar pela letra a, que pede pra gente a transitividade do material.
Podemos encontrar a transitividade assim, olha só:
Para achar os valores de e , vamos calcular:
E visitando a tabela 12.2, temos que:
Agora sim podemos achar a transitividade:
Passo 2
Na letra b, o enunciado quer que a gente encontre a temperatura em que será atingido o regime estacionário… Podemos achar usando essa relação aqui:
Precisamos encontrar duas coisinhas que estão faltando aí… o e o :
Ops! Ainda tá faltando gente aí!
Vamos voltar lá:
E agora sim, voltando na equação para encontrar a temperatura vamos ter:
ou
Show! Agora pra fechar… Letra c!
Passo 3
Na letra c, vamos achar a transferência de calor radiante: