Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 40

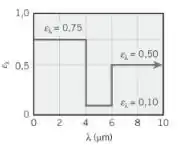
Uma superfície difusa é caracterizada pela distribuição de emissividades hemisféricas espectrais mostrada na figura. Considerando temperaturas superficiais na faixa de 300 ≤ Ts ≤ 1000 K, em qual temperatura o poder emissivo será minimizado?

Passo 1

Bom, pra determinar o que o nosso enunciado está pedindo vamos usar a equação 12.43:

ε T = ∫ 0 ∞ ε λ   .   E λ ,   b   .   d λ E b T

ε T = ε 1   .   ∫ 0 λ 1   E λ ,   b   .   d λ   +   ε 2   .   ∫ 0 λ 2   E λ ,   b   .   d λ   +   ε 3   .   ∫ 0 λ 3   E λ ,   b   .   d λ E b T

ε T = ε 1   .   F 0 → 1,5   +   ε 2   .   F 0 → λ 2 -   F 0 → λ 1   +   ε 3   .   1 -   F 0 → λ 2

Tendo λ 1 = 4   μ m , λ 2 = 6   μ m , ε 1 = 0,75 , ε 2 = 0,10 e ε 3 = 0,50 , ainda precisamos encontrar o valor de F 0 → 4 e F 0 → 6 , pra isso vamos calcular:

λ   .   T = 4   .   300 λ   .   T = 6   .   300

λ   .   T = 1200   μ m   .   K λ   .   T = 1800   μ m   .   K

E visitando a tabela 12.2, temos que:

F 0 → 4 = 0,002134 F 0 → 6 = 0,039341

Então vamos encontrar nossa emissividade:

ε 300 = 0,75   .   0,002134   +   0,10   .   0,039341 - 0,002134   +   0,50   .   1 - 0,039341

ε 300 = 0,486

E vamos ter então um poder emissivo de:

E ( 300 ) = ε 300   .   σ   .   T 4

E ( 300 ) = 0,486   .   5,67   .   10 - 8   .   300 4

E ( 300 ) ≈ 223   W / m ²

Passo 2

Se a gente monta um gráfico do nosso poder emissivo, na faixa de temperatura que foi dada no enunciado, 300   K   ≤   T s   ≤   1000   K , vemos o seguinte:

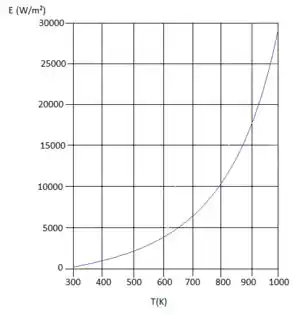
E podemos responder que a temperatura onde se encontra o nosso menor poder emissivo é em:

T = 300   K

Uhul! Conseguimos!!

Resposta

A temperatura onde se encontra o nosso menor poder emissivo é T = 300   K .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46 - Para um comprimento de onda λ especificado, medidas da intensidade espectral I λ , e ( λ ,T )=ε λ I λ , c n da radiação emitida por uma superfície difusa podem ser usadas para determinar a temper
45 - Um termômetro de radiação é um instrumento que responde a um fluxo radiante em um intervalo espectral estabelecido e é calibrado para indicar a temperatura de um corpo negro que produz o mesmo fl
50 - Um pequeno objeto opaco e difuso, a T s = 400K , está suspenso em um grande forno cujas paredes internas estão a T f = 2000K . As paredes são difusas e cinzas, e têm uma emissividade de 0,20 . A
58 - Considere uma superfície difusa e opaca com a absortividade espectral e a irradiação apresentadas a seguir:Qual é a absortividade total da superfície para a irradiação especificada? Se a superfíc
47 - O aço laminado que emerge da seção de laminação a quente de uma usina siderúrgica tem uma temperatura de 1200K , uma espessura δ = 3m m e a seguinte distribuição para a emissividade hemisférica e