Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 41
Considere a superfície direcionalmente seletiva que tem a emissividade direcional εθ mostrada a seguir.
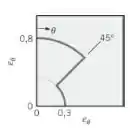
Supondo que a superfície seja isotrópica na direção ϕ, calcule a razão entre a emissividade normal εn e a emissividade hemisférica εh.
Passo 1
Pra gente resolver precisamos primeiro encontrar a emissividade, ok?
Vamos então usar a equação 12.42:
Prontinho! Agora vamos achar a razão que o exercício quer!
Passo 2
Nossa razão será:
Show! Conseguimos!
Resposta
Exercícios de Livros Relacionados
A absortividade espectral α λ e a refletividade espectral ρ λ de um material difuso espectralmente seletivo são mostradas a seguir.(a) Esboce a transmissividade espectral τ λ .(b) Se irradiação solar
53 - Seja o Problema 4.51.(a) Os estudantes receberam, cada um, um espelho de prata, plano e de primeira superfície, com os quais, coletivamente, irradiam o navio de madeira no local B. A reflexão no
56 - A absortividade hemisférica espectral de uma superfície opaca tem o comportamento mostrado a seguir.Qual é a absortividade solar, α S ? Se for considerado que ε λ = α λ e que a superfície se enco
44 - Estime a emissividade hemisférica total ε de aço inoxidável polido a 800K , usando a Equação 12.43 com as informações fornecidas na Figura 12.17. Suponha que a emissividade hemisférica é igual à
51 - A distribuição da refletividade espectral de uma tinta branca (Figura 12.22) pode ser aproximada pela seguinte função degrau:Uma pequena placa plana revestida com essa tinta encontra-se suspensa