Ar entra em um bocal convergente-divergente a com velocidade desprezível. Considerando o escoamento isentrópico, determine a contrapressão que resultará em um número de Mach de saída de .

Essa é uma questão sobre escoamento isentrópico (escoamento com entropia constante) de gás ideal (ar) através de um bocal convergente-divergente. A questão pede para a gente calcular quanto vale a pressão do ar na saída do bocal, sabendo que a velocidade do ar na entrada do bocal vale zero e que a pressão do ar na entrada do bocal vale .

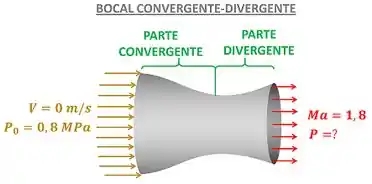
é o número de Mach da saída do bocal que foi dado pelo enunciado.

Vemos pela figura acima, identificamos as propriedades onde com um zero abaixo delas. Chamamos as propriedades de um fluido, quando , de propriedades de estagnação. Por isso a pressão da entrada é identificada como e é chamada de pressão de estagnação!

Logo, temos a pressão de estagnação do ar e queremos a pressão . Então, para achar precisamos de uma equação que relacione a pressão com a pressão de estagnação . Essa equação é a equação 12-19 do livro.

onde é a razão de calores específicos do gás ideal que vale para ar.